Skip to content

DFT例题

约 513 个字 3 行代码 2 张图片 预计阅读时间 3 分钟

讨论

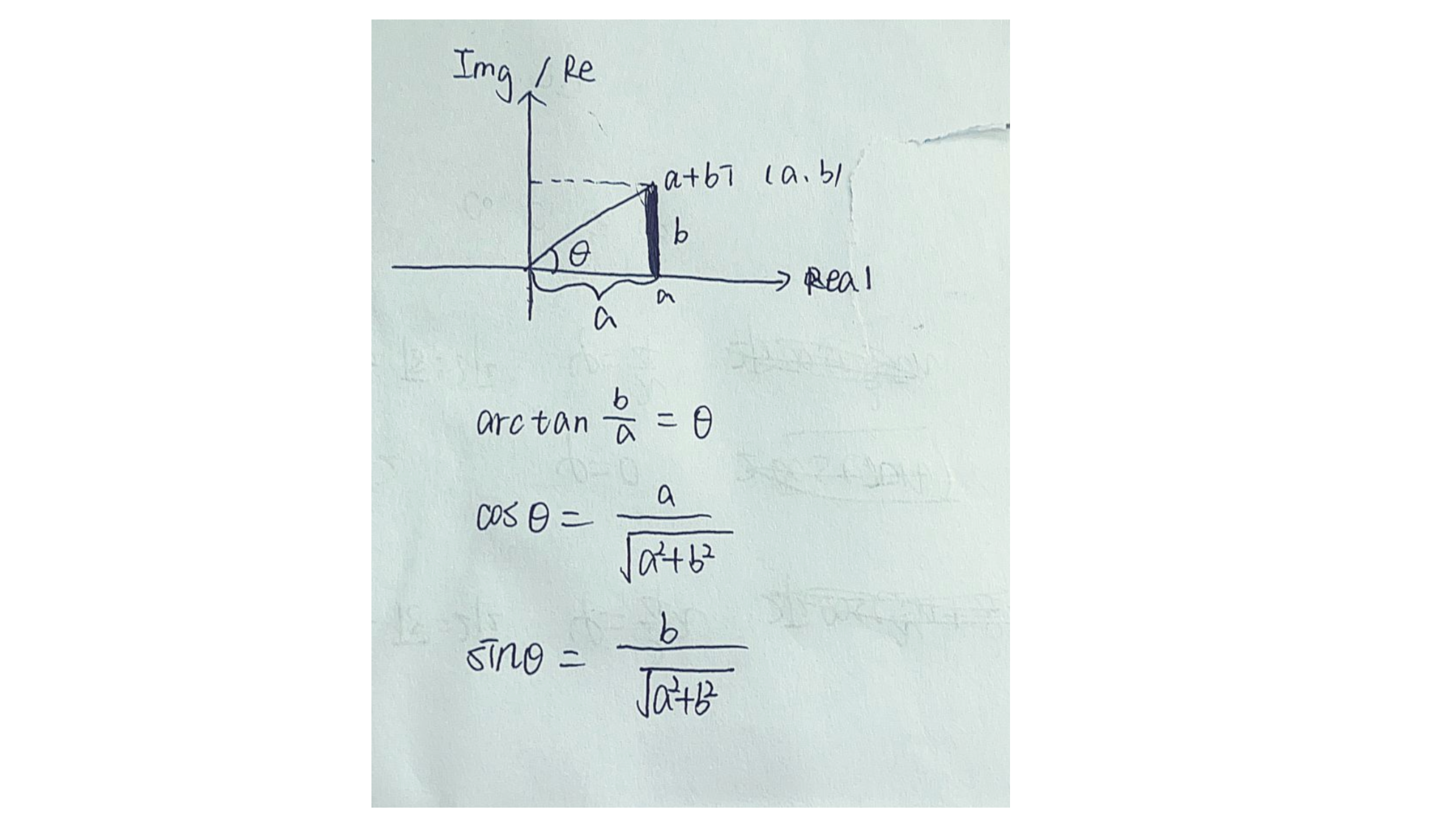
复数、复指数、三角函数的相互对应

\(a+bi\)

= \(\sqrt{a^2 + b^2} e^{i {arctan\frac{b}{a}}}\)

= \(\sqrt{a^2 + b^2}(\cos {(\arctan\frac{b}{a})}+ i \sin {(\arctan\frac{b}{a})} )\)

\(\cos {(\arctan\frac{b}{a})} = \frac{a}{\sqrt{a^2 + b^2}}\)

\(\sin {(\arctan\frac{b}{a})} = \frac{b}{\sqrt{a^2 + b^2}}\)

图形：

image-20250330163847048

问题描述：

对[4,3,2,1]进行 DFT

Python
from scipy.fft import fft
fft([4,3,2,1])

out：

Python
array([10.-0.j,  2.-2.j,  2.-0.j,  2.+2.j])

数学上的计算：

  • \(N=4\)，基波频率 \(\Omega = \frac{2\pi}{N} = \frac{\pi}{2}\)，基波分量为：\(1\Omega n\)
  • 谐波频率分别为：$2\Omega $ 、$3\Omega $
  • 谐波分量（\(k\Omega n\)）分别为：$2\Omega n $ 、 $ 3\Omega n $

利用公式：\(X[k]=w^{kn}x_n\)

\(w=e^{-i\Omega} = e^{-i\frac{\pi}{2}}=-i\) 几何意义，复平面反方向旋转 90°

\[ w^{kn} = \begin{bmatrix} w^{0×0} & w^{0×1} & w^{0×2} & w^{0×3}\\w^{1×0} &w^{1×1} & w^{1×2} & w^{1×3}\\w^{2×0} & w^{2×1} & w^{2×2} & w^{2×3}\\w^{3×0} &w^{3×1} & w^{3×2} & w^{3×3} \end{bmatrix} \\\\\quad = \begin{bmatrix} w^{0} & w^{0} & w^{0} & w^{0}\\w^{0} & w^{1} & w^{2} & w^{3}\\w^{0} & w^{2} & w^{4} & w^{6}\\w^{0} & w^{3} & w^{6} & w^{9} \end{bmatrix} \quad = \begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & w^{1} & w^{2} & w^{3}\\1 & w^{2} & w^{4} & w^{6}\\1 & w^{3} & w^{6} & w^{9} \end{bmatrix} \\\\= \begin{bmatrix} 1 & 1 & 1 & 1\\1 & -i & i^{2} & -i^{3}\\1 & i^{2} & i^{4} & i^{6}\\1 & -i^{3} & i^{6} & -i^{9} \end{bmatrix} \]

关于复数 \(i\) 的周期性：

  • \(i^{0}=i^{4n}=1\)
  • \(i^{1}=i^{1+4n}=i\)
  • \(i^{2}=i^{2+4n}=-1\)
  • \(i^{3}=i^{3+4n}=-i\)

所以：

\[\begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & -i & i^{2} & -i^{3}\\1 & i^{2} & i^{4} & i^{6}\\1 & -i^{3} & i^{6} & -i^{9} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1\\1 & -i & i^{2} & -i^{3}\\1 & i^{2} & i^{4} & i^{2}\\1 & -i^{3} & i^{2} & -i \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1\\1 & -i & -1 & -i\\1 & -1 & 1 & -1\\1 & -i & -1 & -i \end{bmatrix}\]

所以 DFT：

\[\begin{bmatrix} 1 & 1 & 1 & 1\\1 & -i & -1 & i\\1 & -1 & 1 & -1\\1 & i & -1 & -i \end{bmatrix}\begin{bmatrix} 4\\3\\2\\1 \end{bmatrix}=\begin{bmatrix} 10\\4-3i-2+i\\4-3+2-1\\4+3i-2-i \end{bmatrix}=\begin{bmatrix} 10\\2-2i\\2\\2+2i \end{bmatrix}\]

它的复指数形式、三角函数形式、辅助角形式以及对应的：幅度谱、相位谱

image-20250327100625932

目前，分析到这里，还有一些比较奇怪的地方

add_circle2025-03-27 08:50:24update2025-03-30 16:39:01