参考文献:
- 基于时间序列生成对抗网络的滑坡位移预测
- 基于二次分解策略和 IWOA-GRU 的城市道路短时交通流预测研究
- 基于序列分解法的混合模型在时间序列预测中的应用
- 结合模态分解和时间序列预测的方法及在海浪波高预测应用
分解算法介绍
总结:
- 全称
- 关系定义法(与其他的对比)
- 自己的定义(算法步骤)(算法流程图)
- 与其他的优缺点
自适应噪声完备集合经验模态分解
- 时间序列分解技术将复杂的序列分解成多个较为平稳的子序列,使得模型可以更好的学习到平稳序列的规律,预测也可以更加准确
- 经验模态分解,时序预测,序列的平稳化
- 自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)(EMD,EEMD)
- CEEMDAN, 向原始信号中加入高斯白噪声序列,弱化原始序列中的噪声
- EMD,EEMD, 模态分解和分解不充分的问题
- 三种分解算法的目的都是为了使得分解后的子序列更加平稳
EMD
经验模态分解(Empirical Mode Decomposition,EMD)
-
提高序列平稳性
-
复杂序列分解为几个相对平稳的子序列
-
定义:
通过经验,识别原始序列内在的固定属性,将一个序列分解为有固定频率的分量,且分量必须满足的条件:
(1)总极值点和 0 的交叉个数应该等于 1 或者最多相差 1
(2)由局部极值点形成的上下包络线的平均值始终等于 0
- 分解的步骤(六步):
(1)找到原始序列 $X(t)$ 的所有极大值点和极小值点
(2)对极大值和极小值进行三次样条插值,生成上包络线和下包络线
(3)根据上下包络线的逐点平均计算局部平均级数 $m$
(4) 从 $X(t)$ 中减去 $m$,得到一个候选本征模态函数 $IMF$
$$ h=X(t)-m $$(5)检查 $h$ 的属性 :
① 如果 $h$ 不是 $IMF$ (不满足前面的定义), 则用 $h$ 替换 $X(t)$ ,并重复步骤 1
② 如果 $h$ 是一个 $IMF$ , 则计算剩余的信号:
$$ r = X(t)-h $$(6) 通过分解剩余信号,重复步骤 1 到步骤 5,当残差 $r$ 满足预定义的准则时,分解结束.
最终分解后得到了一个残差项 $r$ 和 $n$个 $IMF$ 的集合,命名为 $h_i(i=1,2,...,n)$ , 将生成的 $h_i$ 按频率降序排列, 则 $h_1$ 是与局部相关联的频率最高的一个子序列,此外原始序列 $X(t)$ 可以通过 线性叠加精准的重建:
$$ X(t)= \sum_{i=1}^n h_i + r $$- EMD的局限:
(1) 分解后的子序列可能会出现模态混淆问题,即同一个子序列中可能会出现几种变化频率
(2)分解过程需要重复迭代,导致分解时间较长,分解效率低
EEMD
- 全称
集合经验模态分解
Ensemble Empirical Mode Decomposition,EEMD
- 相对于 EMD 的改进:
在总体平均之前添加白噪声干扰原始序列,然后对原始序列进行集合平均,避免 EMD 子序列的模态混淆问题,使得分解后的子序列更加彻底,平稳
- EEMD 分解流程:
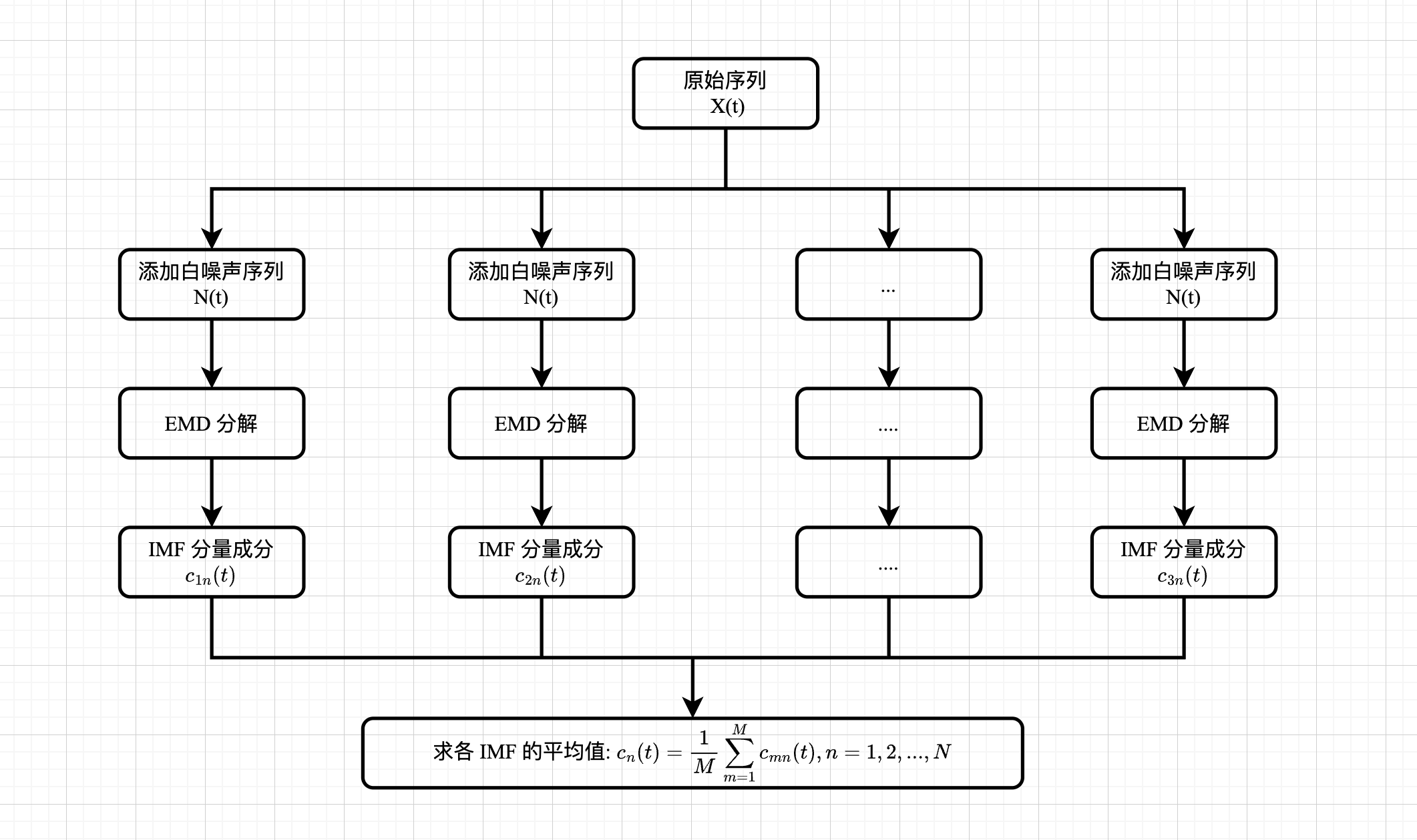
- 分解步骤:
(1) 设定待分解序列的处理次数 $m$
(2)向原始序列中添加 $m$ 个服从正态分布的随机噪声白噪声序列,得到 $m$ 个待分解的新序列
(3) 对每一个新序列分别进行 EMD 分解,得到多个 $IMF$ 分量
(4)对相应模态的 $IMF$ 分量分别求均值,得到最终的 $EEMD$ 分解结果
- 跟 EMD 对比
- 在原始序列中添加白噪声序列可以为 EMD 的分解提供相对一致的分解标准,保证分量的连续性,降低分量模态混淆的概率(EMD,分量模态混淆)
- EEMD 提高了分解结果的精确性,但是 EEMD 添加的白噪声序列得到的集合 平均后也不能完全消除,从而导致分解误差
CEEMDAN
- 全称
- 自适应噪声完备集合经验模态分解
- Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
- CEEMDAN
- 解决 EMD,EEMD 中的模态混淆和残差残余问题
- 分解步骤 :
(1) 向原始序列$X(t)$ 中 添加多个高斯白噪声序列,
$$ X_i(t)= X(t)+\omega_0\cdot n_i(t) $$其中, $X_i(t)$为第 $i$ 次加入高斯白噪声后得到的新序列, $\omega_0$ 为噪声序列的系数
(2)对每个 $X_i(t)$ 进行 EMD 分解,并计算均值,得到的结果即为第一个 CEEMAN 分量
$$ IMF_1 = \frac{1}{M}\sum_{i=1}^M c_{i1} $$其中, $c_{i1}$ 是第一次进行高斯白噪声分解相加后得到的第一个 $IMF$, $M$ 为高斯白噪声的相加次数
(3) 从原始序列 $X(t)$ 中 减去 $IMF_1$ ,得到第一个残差序列:
$$ r_1 = X(t) - IMF_1 $$(4)使用 EMD 继续对 $r_1 + \omega_1 E_1[n_i(t)]$ 进行分解,得到第二个 CEEMDAN 分量,结果如下:
$$ IMF_2= \frac{1}{M}\sum_{i=1}^M E\{r_1(t)+\omega_1E_1[n_i(t)]\} $$其中, $E_j(\cdot)$ 表示由 $EMD$ 分解得到的第 $j$ 个 $IMF$ 分量
(5)重复上述步骤,并计算每一次得到的残差序列,得到剩余的 $IMF$
$$\begin{cases} r_k(t)=r_{k-1}(t)-IMF_k \\ IMF_k=\frac{1}{M}\sum_{i=1}^ME_1\{r_k(t)+\omega_kE_k[n_i(t)]\} & \end{cases}$$其中, $k$ 表示 $IMF$ 分量的总个数
(6)最后,得到所有 CEEMDAN 分量与残差序列的关系:
$$ X(t) = \sum_{i=1}^k IMF_i + res $$- CEEMDAN分解的优势 :
(1)分解更完备:分解后的子序列能更好的保留原始序列的特征
(2)分解效率高:不需要进行太多次迭代就可以完成分解,分解时间短
(3)分解效果好:不容易出现模态混淆和噪声残余问题
VMD
- 全称
- 变分模态分解
- Variational Mode Decomposition
- VMD
- 自适应非递归信号分解方法
- 定义:
通过确定有限带宽下的频率,将原始序列分解为一系列分量,并迭代搜寻变分模态的最优解
- 求解步骤:
(1) 将一个约束变分问题表示如下:
$$\begin{cases} \min_{\nu_k,\omega_k}\left\{\sum_{k=1}^K\left\|\partial k\right[\left(\delta(t)+\frac{j}{\pi t}\right)\otimes\nu_k(t)\right]e^{-j\omega_kt}||_2^2 \} \\ s.t.\sum_{k=1}^K\nu_k=x(t) & \end{cases}$$其中, $x(t)$ 表示 原始序列; $t$ 表示时间; $K$ 表示分解的模态数; $v_k=\{v_1,v_2,...,v_K\}$ 表示第 $k$ 个本征模态分量 ; $\omega_k=\{\omega_1,\omega_2,..,\omega_K\}$ 为第 $k$ 个模态函数的中心频率; $\int_{-\infty}^{+\infty}\delta(t)dt=1$; $\otimes$ 为卷积算子
(2)为了将约束问题 转化为无约束问题,引入了拉格朗日算子 $\lambda(t)$ 和二次惩罚因子 $\alpha$ ,以便于对分解分量进行求解:
$$ L(\{u_k\}, \{\omega_k\}, \lambda(t)) = \alpha \sum_{k=1}^{K} \left\| \partial k \left[ \left( \delta(t) + \frac{j}{\pi t} \right) \otimes v_k(t) \right] e^{-j\omega_k t} \right\|_2^2\\+ \left\| x(t) - \sum_{k=1}^{K} v_k(t) \right\|_2^2 + \langle \lambda(t), x(t) - \sum_{k=1}^{K} u_k(t) \rangle $$(3) 利用乘子交替方法进行求解,调节各模态分量及其中心频率,得到最优的 $v_k,\omega_k, \lambda(t)$ , 对于三者的求解如下:
$$ \hat{v}_k^{n+1} = \frac{\hat{x}(\omega) - \sum_{i \neq k} \hat{v}_i(\omega) + \frac{\hat{\lambda}(\omega)}{2}}{1 + 2\alpha(\omega - \omega_k)^2} \\ \hat{\omega}_k^{n+1} = \frac{\int_0^{\infty} \omega \left| \hat{v}_k^{n+1}(\omega) \right|^2 d\omega}{\int_0^{\infty} \left| \hat{v}_k^{n+1}(\omega) \right|^2 d\omega} \\ \lambda^{n+1}(\omega) = \lambda^n(\omega) + \tau(x(\omega) - \sum_k v_k^{n+1}) $$式中, $n$ 表示迭代次数; $\hat{x}(\omega),\hat{v}_i(\omega),\hat{\lambda}(\omega),\hat{v}_k^{n+1}$ 分别表示 $x(t),v_i(t),\lambda(t),v_k^{n+1}(t)$ 的傅里叶变换系数
样本熵
- 全称
- 样本熵
- Sample Entropy
- SE
🚩 why?
原始序列经过 CEEMDAN 分解后会得到多个子序列,而子序列之间可能存在一定的依赖性,若对每个子序列直接进行预测,会放大误差,因此本文引入样本熵来对子序列的复杂度进行量化,并将其作为 VMD 分解的依据
- SE 值越大,说明子序列的复杂度越高,则需要对该子序列进行再次分解
🚩 HOW?
关于样本熵的计算:
前提:给定一个时间序列 $x(t)=x(1),x(2),x(3),....,x(N)$
其中, $N$ 为样本量, $t=1,2,...,N-1,N$,则序列SE的计算过程如下:
(1)将原始序列 $X(t)$ 转化为 一个 $m$ 维的向量 $X_m(1),X_m(2),...,X_m(N-m+1)$ , 其中:
$X_m=\{x(i),x(i+1),...,x(i+m-1)\},i=1,2,...,m-1,m$
(2)定义向量 $X_m(i)$ 与 $X_m(j)$ 之间的距离为:
$$ ||X_m(i),X_m(j)||=\max_{0\leq k \leq m-1} |x(i+k)-x(j+k)| $$其中,$k=1,2,...,m-1,m$
(3)对任意一个 $X_m(i)$,定义每个 $X_m(i)$ ,定义每个 $X_m(i)$ 和 $X_m(j)$ 之间的距离小于或等于 $r$ 的个数表示 $B_i$, 计算公式 如下:
$$ B_i^m(r) = \frac{1}{N-m-1}B_i\\ B^m(r) = \frac{1}{N-m}\sum_{i=1}^{N-m}B_i^m(r) $$(4)当维数增加到 $m+1$ 时,同理,定义 $X_{m+1}(i)$ 和 $X_{m+1}(j)$之间距离小于或等于 $r$ 的个数表示为 $S_i$, 计算公式如下:
$$ S_i^m(r)= \frac{1}{N-m-1}S_i \\ S^m(r) = \frac{1}{N-m}\sum_{i=1}^{N-m}S_i^m(r) $$(5)最后,计算分量的样本熵:
$$ SE(m,r)=lim_{N\rightarrow \infty} \{-ln[\frac{S^m(r)}{B^m(r)}]\} $$(6) $N$确定时,样本熵为:
$$ SE(m,r,N)=-ln[\frac{S^m(r)}{B^m(r)}] $$式中, $m$ 表示 序列嵌入维度, $r$ 表示 相似容量, $S(m,r)$ 表示 原始序列的样本熵, 原始序列的样本熵大小和 $m,r$的取值 有关.
一般 $m$ 取 $1$ 或者 $2$,$r=(0.1\sim 0.25)SD$
变分模态分解
叙述逻辑
(1)由谁提出?几几年?
(2)解决了前人的什么问题
(3)定义
(4)计算流程图
(5)步骤
(6)优点,评价&不足
- VMD 的核心理念: 任何给定的信号均可视为一系列特定中心频率,有限带宽的子信号(IMFs)合成,
- 该方法依托泛函分析中的变分理论,以经典维纳滤波为基石,通过迭代优化寻找变分模态的最优解,从而在频域中分离并确定各中心频率所对应的信号成分,在迭代过程中,各模态函数及相应中心频率不断更新,最终导出一组具有特定带宽的模态函数
- VMD 的分解本质是一个变分问题的构建和求解过程, 该变分问题旨在寻找泛函的极值,该极值意义在于使所有模态分量的中心频率带宽之和达到最小
- 求解过程中,遵循两方面约束:
(1)确保所有模态分量中心频率带宽总和最小化
(2)保证所有模态分量之和恰好等于原始信号
- 在 VMD 的框架内,定义本征模态函数(IMF)为调幅-调频信号 $u_k(t)$ :
其中:
① 瞬间相位 $\phi_k(t)$ 为非递减函数
②瞬间幅值 $A_k(t)$ 是信号 $u_k(t)$的包络幅值
在变分问题的框架下,为达成信号的自适应分解目标, $VMD$过程的关键环节之一便是求解满足约束条件的变分模型最优解,约束变分模型:
$$ \left\{ \begin{aligned} & \min \left\{ \sum_{k=1}^{K} \left\| \partial_t \left[ \left( \sigma(t) + \frac{j}{\pi t} \right) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 \right\} \\ & \quad \text{s.t.} \sum_{k=1}^{K} u_k = f(t). \end{aligned} \right. $$符号说明:
$$ \begin{equation} L(\{u_k\}, \{\omega_k\}, \lambda) = \alpha \sum_{k=1}^{K} \left\| \partial_t \left[ \left( \sigma(t) + \frac{j}{\pi t} \right) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 + \end{equation} $$$$ \begin{equation} \left\| x(t) - \sum_{k=1}^{K} u_k(t) \right\|_2^2 + \left\langle \lambda(t), f(t) - \sum_{k=1}^{K} u_k(t) \right\rangle. \end{equation} $$
- $\partial_t$ 为梯度运算
- $*$ 卷积运算
- $\sigma(t)$ 狄克拉函数
- $\{u_k\}$ 表示分解后得到的分量
- $\{\omega_k\}$ 表示的 各 $IMF$ 分量的中心频率
- $(\sigma(t)+\frac{j}{\pi t})* u_k(t)$ 表示各 $IMF$ 分量的中心频率
- $||\cdot||_2^2$ 表示 $L_2$ 范数
- 经过上式,原始信号 $f(t)$ 会被分解为 $K$ 个 $IMF$ 分量
- 将有约束变分问题转化为 无约束形式,引入二次惩罚因子 $\alpha$ 及拉格朗日乘子 $\lambda_t$ ,得到增广拉格朗日表达式 :
符号说明
- $\alpha$ ,分解参数,用处:抑制高斯噪声对分解过程的干扰
- 通过拉格朗日乘子 $\lambda_t$ ,运用交替乘子法(ADMM)求得无约束模型的鞍点,可得到最优解,进而将原始信号 $f(t)$ 分解为 $K$ 个具有不同频率特征的分量
- 关于 $IMF$ 分量的讨论
- 各 IMF 分量的频带宽度受 $\alpha$ 参数的二次惩罚项调控
- 若 $\alpha$ 取值过小,各 IMF 带宽扩大,容易导致各分量间相互渗透,增加噪声含量
- 若 $\alpha$ 取值过大,各 $IMF$带宽缩小,可能造成部分真实信号损失
- 关于模态分量数目 $K$ 的选择,参数组合 $(k,\alpha)$ 的选择至关重要
问题引出: 传统 VMD 分解方法中,惩罚因子 $\alpha$ 与分解层数 $k$ 需人工设定, 仅凭经验难以达到最佳分解效果,因此,对参数组合 $(k,\alpha)$ 的优化
参数优化
- 基于鲸鱼智能优化算法的变分模态分解
- 使用 WOA(鲸鱼智能优化算法)对 VMD 的参数组合$(k,\alpha)$ 进行寻优,使用 熵 作为衡量优化程度的标准
- 熵是衡量信息内容的关键指标
高熵表示系统的信息量繁杂,难以预测准确
如果系统的后续状态可以轻松并准确的从之前状态预测出来,这个系统就叫做 低熵
STL分解法
- 全称
- STL
- Seasonal and Trend decomposition using LOESS
- 定义 : 时间序列分解技术, 将时间序列分解为季节项,趋势项,残差项三部分
- 季节项(Seasonal) : STL 方法首先尝试捕捉序列的季节性成分,即数据在一定范围内的周期性变化模式,使用 LOESS(Locally Estimated Scatterplot Smoothing) 方法, 是一种 非参数的局部回归平滑技术,可以有效拟合季节性模式
- 趋势项(Trend) : STL 方法试图捕捉数据的趋势性变化,包括长期趋势,逐年或逐季的整体变化,同样,LOESS方法用于平滑数据以提取趋势
- 残差项(Residual) : 季节项和趋势项序列被从原始序列中移除,得到残差部分,残差项表示无法由季节项和趋势项解释得随机波动或噪声
STL 分解法的分解模式有两种: 加法分解法和乘法分解法
- $Y_t = S_t + T_t + R_t$
- $Y_t = S_t * T_t * R_t$
符号说明
(1) $Y_t$ 原始时间序列
(2) $S_t$ 表示 季节项
(3) $T_t$ 表示 趋势项
(4) $R_t$ 表示 残差项
选哪个?
- 加法模型适合 数据方差随时间变化不大的情况
- 乘法模型适合 数据方差随时间有明显变化的情况
summary : 主要看方差
话术: 考虑到实验数据的方差不会随时间有显著的变化,本文使用加法模型对时间序列进行分解
经验模态分解
- 全称:
- Empirical Mode Decomposition
- EMD
- 经验模态分解
- 经验模态分解的假设
- 任何序列都可以由多个不同的简单波动序列(固有模态)构成
- 每个线性或非线性序列将具有相同的极值和零点
- 在连续的过零点之间,只有一个极值,且各序列相互独立
基于上述假设,每个序列可被分解为多个 IMF(Intrinsic Mode Function,本征模态序列),且每个 IMF 都须满足一下条件:
- 在整个数据集中,极值的个数和零点的个数必须等于或相差 2
- 在任意一点上,有局部最大此定义的包络线和由局部最小值定义的包络线平均值为零
经验模态分解的流程图
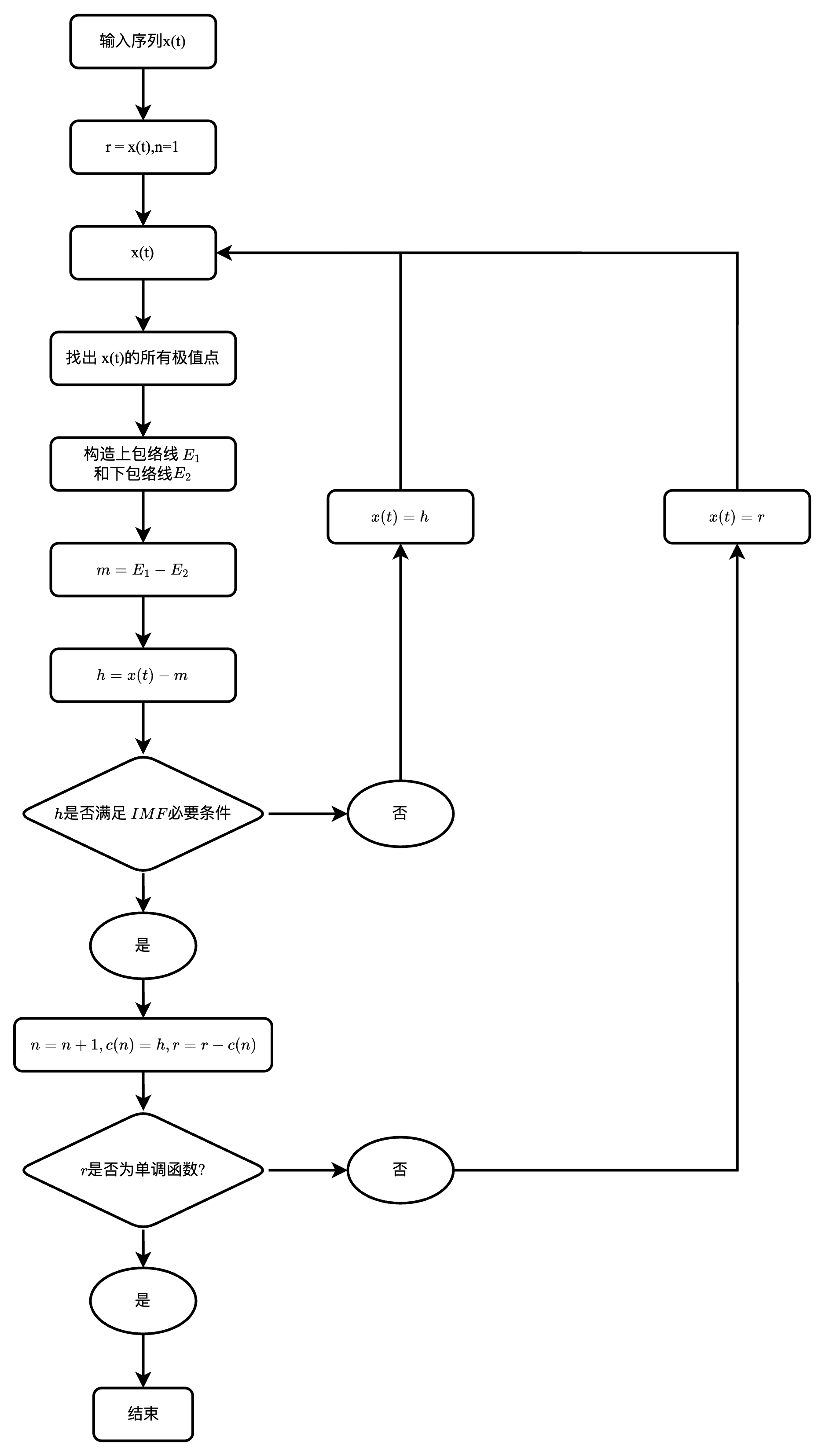
经验模态分解的公式:
$$ x(t)=\sum_{j=1}^n c_j + r_n $$模态分解的关键思想在于通过迭代提取信号中的局部特征,并将其表示为 $IMF$ ,从而实现信号的自适应分解
- IMF
IMF 具有时频性,即在时间和频率上都能适应信号的局部特征
- EMD 具有自适应性和局部特征提取能力在非线性和非平稳序列的分析中得到广泛应用
- EMD 的缺点:模式混合,端点效应,改进: 集合经验模态分解(EEMD),自适应噪声经验模式分解法(CEEMDAN)
完全自适应噪声完备集合 经验模态分解
- 全称:
- 谁提出
- 简写: CEEMDAN
- why? 解决经验模态分解中存在的问题: 模态混叠问题
- 分解步骤:
(1) 向原始信号 $x(t)$ 添加 $K$ 次均值为 0 的高斯白噪声,构造共 $K$ 次实验的待分解序列 $x_i(t)$ ,其中,$i=1,2,3,...,k$
$$ x_i(t)=x(t) + \varepsilon \delta_i(t) $$其中, $\varepsilon$ 代表高斯白噪声的权值系数; $\delta_i(t)$ 则是第 $i$ 次处理过程中产生的高斯白噪声
(2) 对序列 $x_i(t)$进行 EMD 分解,分解后得到的第 1 个模态分量 IMF 将被提取出来,并取其均值作为 CEEMDAN 分解后得到的第 1 个 IMF
$$ IMF_1= \frac{1}{K} IMF_1^i(t)\\ r_1(t) = x(t)-IMF_1(t) $$式中, $IMF_1(t)$ 表示 CEEMDAN 分解得到的第 1 个模态分量; $r_1(t)$ 表示第 1 次分解后余量信号
(3)在完成 EMD 分解后,向第 j 阶段的余量信号添加特定的噪声,并基于这个处理后的信号继续进行 EMD 分解
$$ IMF_j(t) = \frac{1}{K} \sum_{i=1}^K E_1(r_{j-1}+\varepsilon_{j-1}E_{j-1}(\delta_i(t))) \\ r_j(t) = r_{j-1}(t)-IMF_j(t) $$式中: $IMF_j(t)$ 表示 CEEMDAN 分解后得到的第 j 个模态分量
$\varepsilon_{j-1}$ 是 CEEMDAN 在分解第 $j-1$ 阶段余量信号时加入的噪声的权值系数
$r_j(t)$ 表示 第 j 个阶段余量信号
(4) 迭代停止,如果 EMD 的停止条件得以满足,即 第 n 次分解后的余量信号呈现出单调性,那么迭代过程停止,标志着 CEEMDAN 算法的分解阶段完成