智能算法广泛应用于各个领域:参数优化,故障诊断,图像处理,时序预测
群体智能算法是研究个体的特征以及个体与群体之间相互关系,相应机制的算法
常见的群体智能算法可分为:
- 粒子群优化算法(PSO)
- 蚁群优化算法(ACO)
- 细菌觅食优化(BFO)
- 人工鱼群(AFS)
- 人工蜂群(ABC)
生物优化算法:
- 旗鱼优化算法
- 鲸鱼优化算法
旗鱼优化算法
from : 基于序列分解法的混合模型在时间序列预测中的应用
- 全称:
- Sailed fish optimizer
- SFO
- 谁提出
该算法具有求优能力强,收敛速度快等优点,算法的灵感来源于一群旗鱼捕食者,该策略包含两部分
(1) 改进最佳种群的搜索
(2)为达到沙丁鱼种群的多样性进行拓展搜索空间
得益于双种群模式的设计,该算法在训练速度上要优于许多生物优化算法
旗鱼算法的初始化包括旗鱼的初始化和沙丁鱼的初始化,其初始化是在给定的搜索空间内随机进行的,在第 i 次迭代中适应度最高的精英旗鱼和受伤沙丁鱼的位置分别称为 $X_{\text{elite-SF}}^i$ 和 $X_{\text{injured-S}}^i$
在 SFO 算法中,旗鱼 $ X_{new - SF }^i$ 在第 i 次迭代中的位置更新规则如下式:
$$ X_{new\_SF}^i = X_{elite\_SF}^i -\lambda_i * (rand(0,1)*(\frac{X_{elite\_SF}^i + X_{injured\_S}^i}{2})) $$其中,
- $X_{elite- SF}^i$ 表示到目前为止,精英旗鱼的位置
- $X_{injured-S}^i$ 表示到目前为止,受伤沙丁鱼的最佳位置
- $X_{old-SF}$ 为当前旗鱼的位置
- $rand(0,1)$ 为介于 0 和 1 之间的随机数
- $\lambda_i$ 第 i 次迭代时的系数,计算过程如下:
- 其中, $PD$ 表示猎物群的密度,表达式:
其中:
- $N_{SF}$ 和 $N_S$ 分别表示旗鱼和沙丁鱼的数量
在 SFO 算法中,沙丁鱼 $X_{new-S}^i$ 在第 i 次 迭代中的位置更新规则如下:
$$ X_{new\_S}^i = r \times (X_{elite\_SF}^i-X_{old\_S}^i+AP) $$其中, $X_{elite - {SF}}^i$ 代表当前迭代次数 i 时的最佳位置, $AP$ 代表 旗鱼的攻击强度,计算公式:
$$ AP=A \times (1-(2\times Itr \times \varepsilon)) $$其中, $A$ 和 $\varepsilon$ 是从 $A$ 到$0$ 的线性递减的相关系数, $Itr$ 代表迭代次数
以下是根据特定的任务进行设置:
A 设为4, $\varepsilon$ 设为 0.001,当 $AP\geq 0.5$ ,更新所有沙丁鱼的位置,当 $AP\leq0.5$ 时,只更新沙丁鱼的部分位置,部分位置的范围定义:
$$ \alpha = N_S * AP\\ \beta = d_i * AP $$- $\alpha$ 表示需要更新的沙丁鱼数量
- $\beta$ 表示需要更新的维度数量
- $d_i$ 是第 i 次迭代的变量数量
- $N_S$ 是算法每个循环中的沙丁鱼数量
如果 沙丁鱼的位置优于旗鱼的位置,则沙丁鱼的位置支付给旗鱼并移除,更新过程如下:
$X_{SF}^i = X_S^i,\text{if} \ f(S_i) 使用方法: 在这篇论文中,使用 SFO 算法优先 ESN 初始化权重参数,并搜索 ESN 中三个矩阵参数的最优值,目的是为了使得 ESN 具有最理想的性能 所有旗鱼和沙丁鱼种群的位置都是随时初始化的,每个种群都包含 ESN 中三个初始矩阵($W_{in}$,$W$和 $W_{back}$) 的值. 通过计算不同种群对应的 ESN 训练模型的误差,得出每个种群的适应度 通过迭代,更新每个种群的最佳位置和当前位置,得到最终较为理想的 ESN 模型 from: 基于时间序列生成对抗网络的滑坡位移预测 WOA 2016 年,谁提出, Seyedali Mirjalili WOA 模拟了座头鲸特有的气泡网捕食机制,即座头鲸群体首先在一定区域内探测猎物,定位猎物后,围绕猎物形成螺旋路径,并在猎物周围释放螺旋状气泡网,迫使猎物向气泡网中心聚集,最终捕获猎物 (初始化) 在WOA 中,每只座头鲸的位置被视为一个潜在解,通过随机初始化或以当前最优解为参考进行初始化 (逼近) 算法通过迭代更新座头鲸在解空间中的位置,逐步逼近全局最优解 该算法主要包括三个阶段:围捕猎物,实施气泡网攻击,以及持续追踪猎物 在围捕猎物阶段,WOA 假定当前已接近目标,种群最优个体会被作为追踪目标的参照,该个体位置被视为待优化问题的变量及潜在解 通过不断更新最优个体位置,力求进一步缩小包围圈,是指更贴近目标猎物,公式如下:
其中, $\vec{a}$ 在迭代过程中从 2 下降到 0 $T_{max}$ 是最大迭代次数 $\vec{r}$ 是 $[0,1]$ 中的随机向量,将 $\vec{A}$ 限制在 $[-1,1]$ 气泡网攻击过程即是局部搜索过程,就是以种群中最优的个体为中心,计算最优鲸鱼位置和猎物位置之间的距离,以包围和上升两种方式记录捕食过程,建立等式模仿鲸鱼进行螺旋式搜索,公式:
符号说明 在包围方法中,如果 $|\vec{A}|<1$ ,鲸鱼的下一次位置将位于当前位置与猎物之间的任一位置,逐渐靠近并包围当前最优解,这一过程属于局部搜索阶段 相反,上升策略涉及计算其余鲸鱼与当前最优解的空间距离,随后进行螺旋上升游走,以实施环绕搜索,当前搜索策略的公式:
具体来说: $p$ 表征鲸鱼在不断收窄的圆形区域内的沿螺旋轨迹游动的行为, 此外,鲸鱼亦会进行随机猎物搜寻,即全局搜索阶段, 此时,种群随机选取 非当前最优位置的个体作为追踪对象,并据此调整自身位置进行大范围猎物搜寻,旨在规避陷入局部最优解的局限,公式:
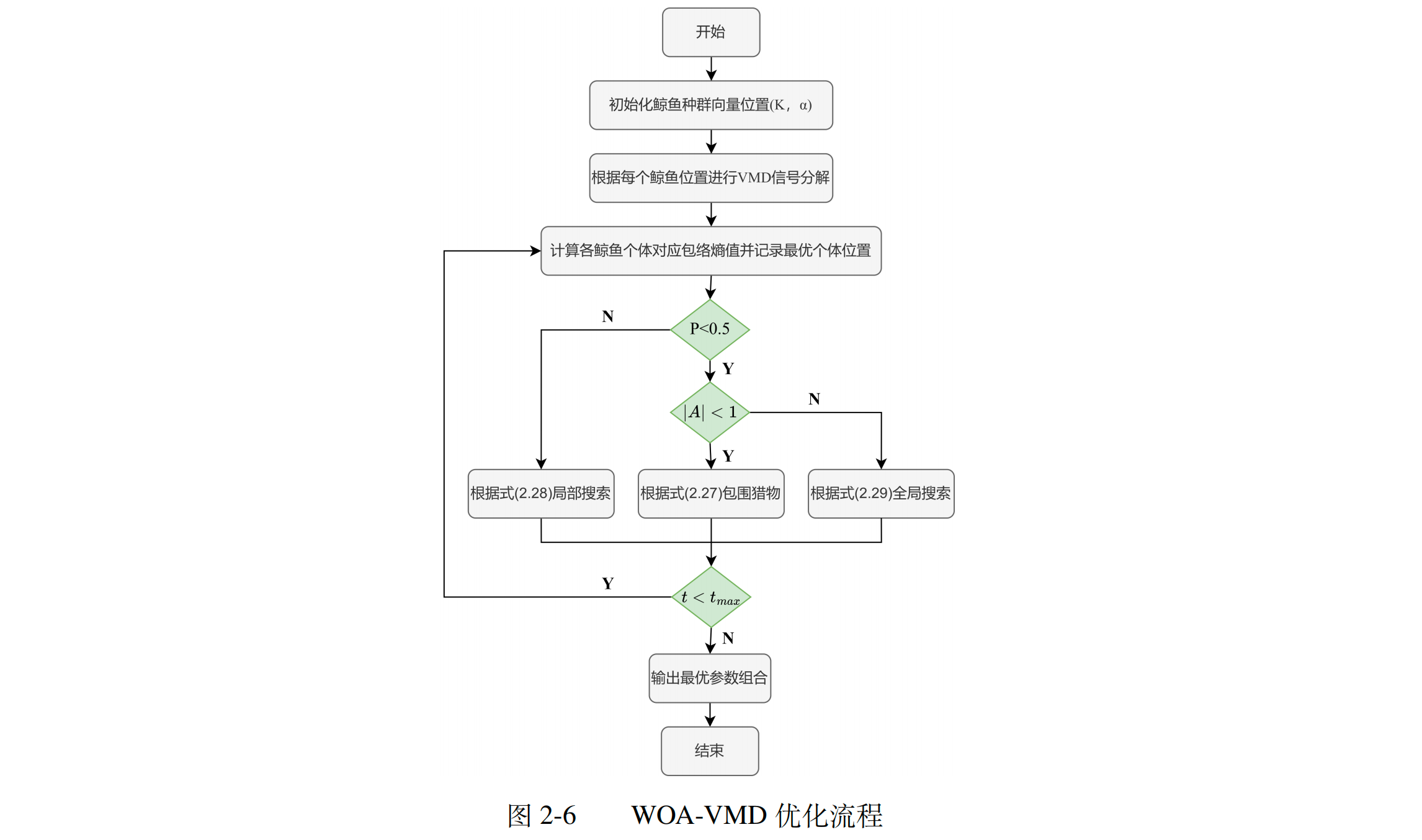
其中, 使用场景: 使用 WOA 对 VMD 的参数组合 $(k,\alpha)$ 进行寻优 采用熵作为衡量优化程度的标准. 熵提供了信息内容的度量, 高熵表示系统的信息繁杂,难以预测精准 反之,如果系统的后续状态可以轻松并准确的从之前状态预测出来,那么这个系统就被成为具有低熵 公式: from: 基于 LSTM 与 Informer 的多模型组合短期电力负荷预测研究 在 $n$ 维空间中,假设存在一个含有 $m$ 个微粒的种群 $X$ , 第 $i$ 个微粒的速度 $V_i$ , 位置为 $X_i$ 在每一次迭代中,通过 目标函数来评价微粒个体最优位置 $P_i$ 和群体最优位置 $P_g$,从而更新各微粒的速度和位置 各微粒速度和位置的迭代更新的计算公式: $V_{id}^{k+1}= \omega V_{id}^k + c_1 r_1(P_{id}^k-X_{id}^k) + c_2r_2(P_{gd}^k-X_{gd}^k)$ 该公式分为三个部分 $X_{id}^{k+1}= X_{id}^k+V_{id}^{k+1}$ 启发式搜索算法,使用进化论的概念寻找问题的最优解或次优解,类似于自然进化鲸鱼优化算法
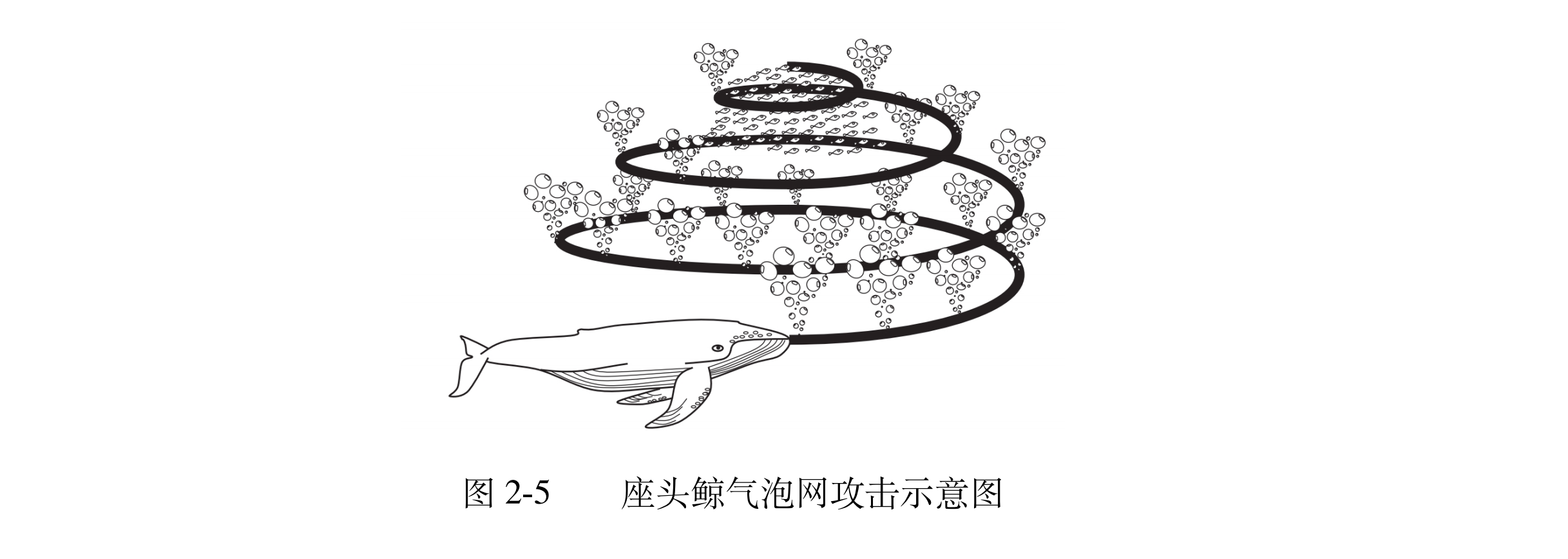
第一阶段 : 捕获猎物阶段
$$
\vec{A} = 2\vec{a}\vec{r}-\vec{a},\\
\vec{C}=2\vec{r},\\
\vec{a}=2-\frac{2t}{T_{max}}
$$
第二阶段: 气泡网攻击过程
第三阶段: 包围方法
鲸鱼优化算法的应用
优化流程
粒子群优化算法
全称
流程图
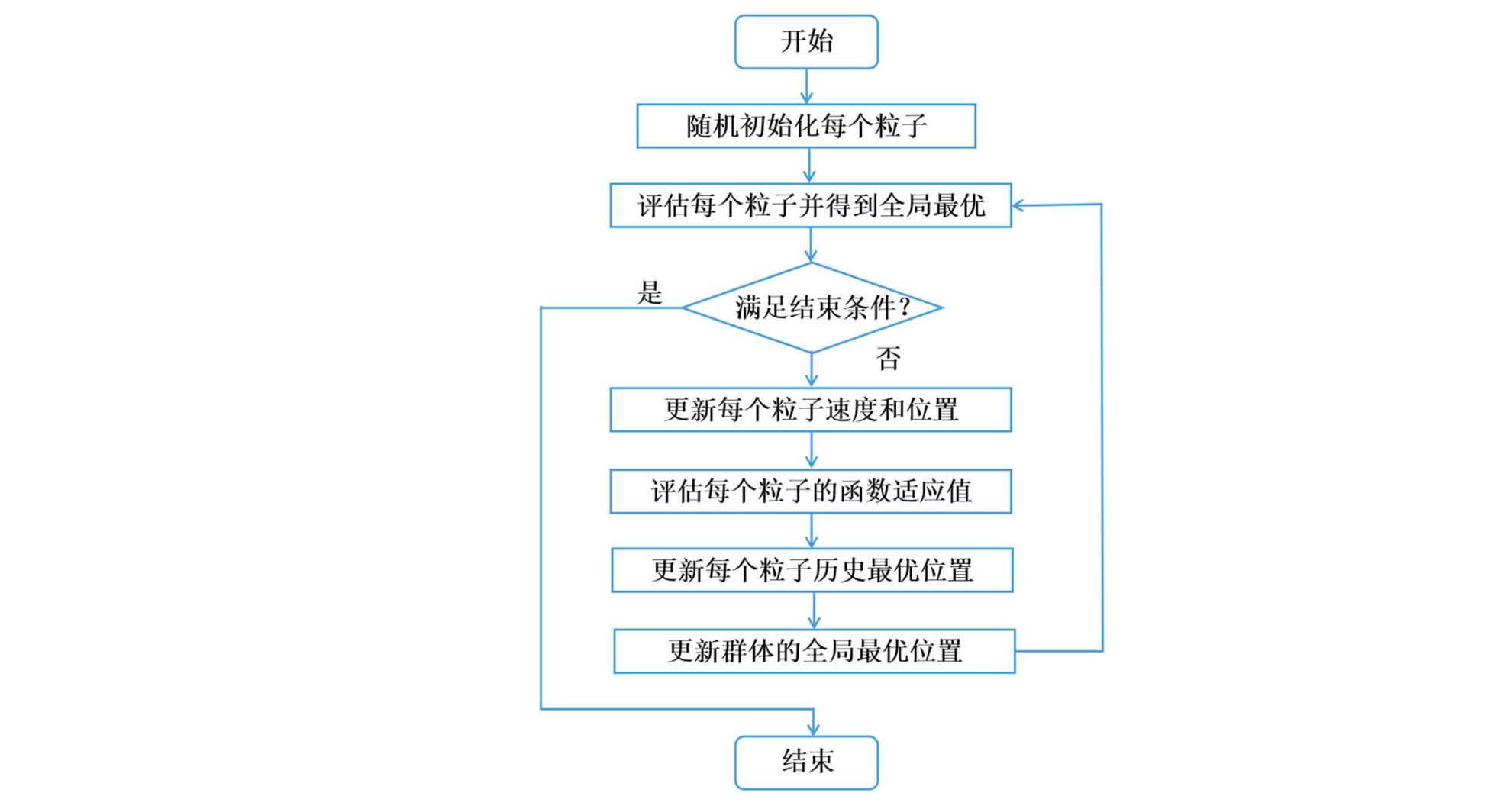
流程说明
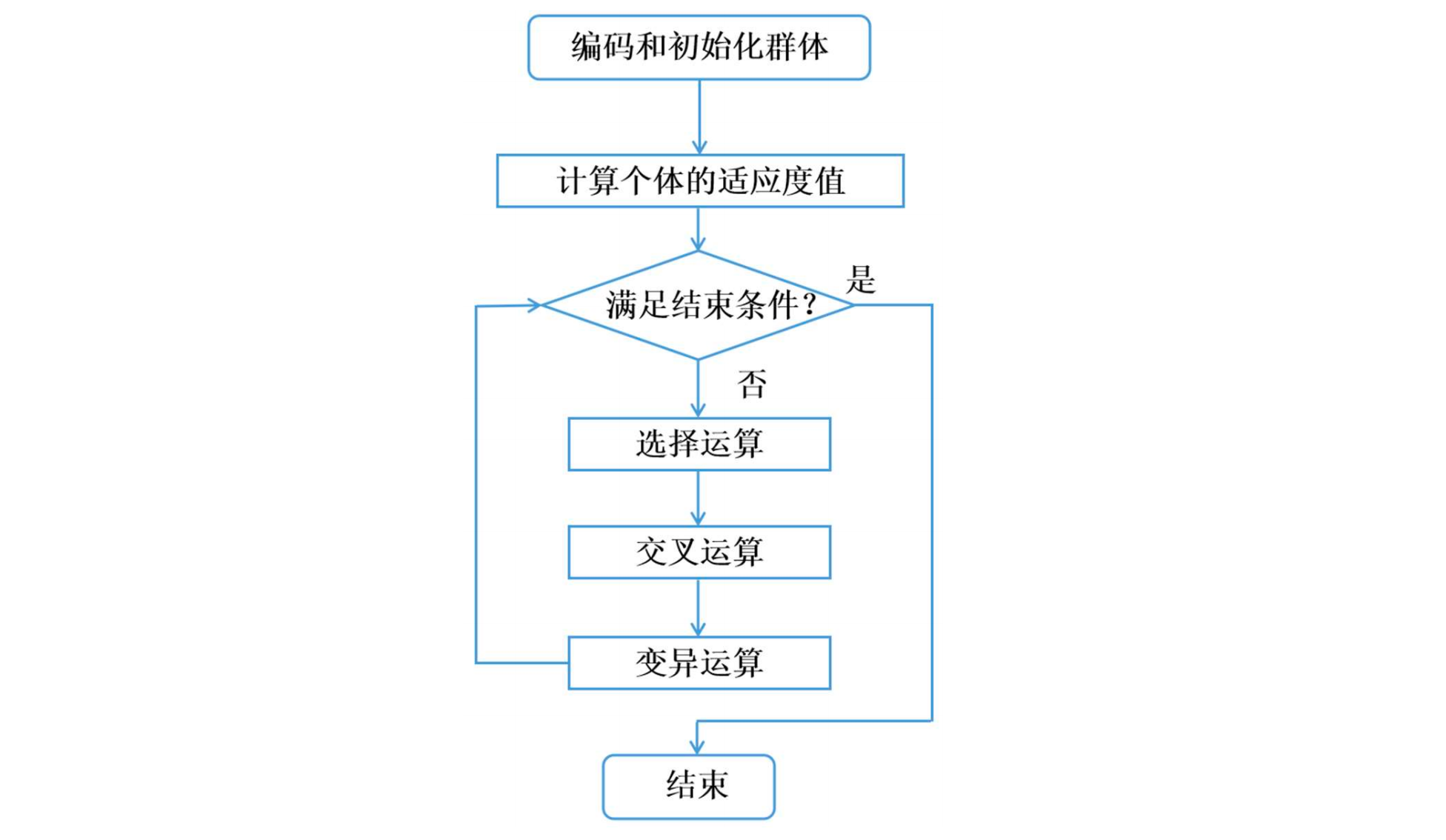
遗传算法
全称
描述
算法流程