2024ICLR、蚂蚁集团、吴海旭

论文：TIMEMIXER: DECOMPOSABLE MULTISCALE MIXING FOR TIME SERIES FORECASTING

代码：https://github.com/kwuking/TimeMixer

• 代码数据流动图

==关键词：==

TimeMixer = PDM + FMM

• 可分解
• 多尺度混合

摘要

Time series forecasting is widely used in extensive applications, such as traffic planning and weather forecasting. However, real-world time series usually present intricate temporal variations, making forecasting extremely challenging.

时间序列预测广泛应用于众多领域，例如交通规划和天气预报。然而，现实世界中的时间序列通常表现出复杂的时间变化，这使得预测极具挑战性。

Going beyond the mainstream paradigms of plain decomposition and multiperiodicity analysis, we analyze temporal variations in a novel view of multiscale-mixing, which is based on an intuitive but important observation that t==ime series present distinct patterns in different sampling scales.==

与传统的简单分解和多周期性分析范式不同，我们从一种新颖的多尺度混合视角来分析时间变化，这种视角基于一个直观但重要的观察结果：时间序列在不同的采样尺度上呈现出不同的模式。

The microscopic and the macroscopic information are reflected in fine and coarse scales respectively, and thereby complex variations can be inherently disentangled.

微观和宏观信息分别反映在细粒度和粗粒度的尺度上，从而可以内在地解耦复杂的变化。

Based on this observation, we propose TimeMixer as a fully MLP-based architecture with Past-Decomposable-Mixing (PDM) and Future-Multipredictor-Mixing (FMM) blocks to take full advantage of disentangled multiscale series in both past extraction and future prediction phases.

基于这一观察结果，我们提出了TimeMixer，这是一种完全基于MLP（多层感知器）的架构，包含Past-Decomposable-Mixing（PDM）和Future-Multipredictor-Mixing（FMM）模块，以充分利用过去提取和未来预测阶段中解耦的多尺度序列。

Concretely, PDM applies the decomposition to multiscale series and further mixes the decomposed seasonal and trend components in fine-to-coarse and coarse-to-fine directions separately, which successively aggregates the microscopic seasonal and macroscopic trend information.

具体来说，PDM对多尺度序列进行分解，并进一步在细粒度到粗粒度和粗粒度到细粒度的方向上分别混合分解后的季节性和趋势成分，从而逐步聚合微观季节性和宏观趋势信息。

FMM further ensembles multiple predictors to utilize complementary forecasting capabilities in multiscale observations. Consequently, TimeMixer is able to achieve consistent state-of-the-art performances in both long-term and short-term forecasting tasks with favorable run-time efficiency.

FMM进一步集成多个预测器，以利用多尺度观测中的互补预测能力。因此，TimeMixer能够在长期和短期预测任务中实现一致的最先进的性能，并且具有良好的运行时效率。

方法

Given a series $x$ with one or multiple observed variates, the main objective of time series forecasting is to utilize past observations (length-$P$ ) to obtain the most probable future prediction (length-$F$ ).

给定一个包含一个或多个观测变量的时间序列 \( x \)，时间序列预测的主要目标是利用过去的观测值（长度为 \( P \)）来获得最有可能的未来预测值（长度为 \( F \)）。

As mentioned above, the key challenge of accurate forecasting is to tackle intricate temporal variations.

如上所述，准确预测的关键挑战在于处理复杂的时间变化。

In this paper, we propose $\text{TimeMixer}$ of multiscale-mixing, benefiting from disentangled variations and complementary forecasting capabilities from multiscale series.

在本文中，我们提出了 TimeMixer，这是一种多尺度混合方法，得益于从多尺度序列中提取的解耦变化和互补的预测能力。

Technically, TimeMixer consists of a multiscale mixing architecture with Past-Decomposable-Mixing and Future-Multipredictor-Mixing for past information extraction and future prediction respectively.

从技术角度来看，TimeMixer 包括一个多尺度混合架构，其中 Past-Decomposable-Mixing 用于提取过去信息，而 Future-Multipredictor-Mixing 用于进行未来预测。

3.1 MULTISCALE MIXING ARCHITECTURE

Time series of different scales naturally exhibit distinct properties, where fine scales mainly depict detailed patterns and coarse scales highlight macroscopic variations (Mozer, 1991).

不同尺度的时间序列自然表现出不同的特性，其中细粒度尺度主要描绘详细的模式，而粗粒度尺度则突出宏观变化（Mozer, 1991）。

This multiscale view can inherently disentangle intricate variations in multiple components, thereby benefiting temporal variation modeling. It is also notable that, especially for the forecasting task, multiscale time series present different forecasting capabilities, due to their distinct dominating temporal patterns (Ferreira et al., 2006). Therefore, we present TimeMixer in a multiscale mixing architecture to utilize multiscale series with distinguishing designs for past extraction and future prediction phases.

这种多尺度视角可以内在地解耦多个组成部分中的复杂变化，从而有利于时间变化建模。值得注意的是，特别是对于预测任务，由于不同的主导时间模式，多尺度时间序列表现出不同的预测能力（Ferreira et al., 2006）。因此，我们提出了TimeMixer，采用多尺度混合架构，利用多尺度序列，并为过去信息提取和未来预测阶段设计了不同的方案。

下采样 嵌入&分解

==（1）分解：==

输入：$x \in \mathbb{R}^{P \times C}$

处理：通过平均池化 分解成 $M$ 个尺度，得到一系列多尺度时间序列

输出：$X = \{x_0,...,x_M\}$

符号说明：

• $x_m \in \mathbb{R}^{\frac{P}{2^m}\times C},m\in\{0,...,M\}$

• $C$是变量个数

• $x_0=x$ 是输入序列，包含最精细的时间特征

• $x_M$ 用于表示宏观变化

==（2）嵌入==

输入：多尺度时间序列的输入 $X^0$ ，分解完以后嵌入

输出：$X^0 = \text{Embed}(X)$

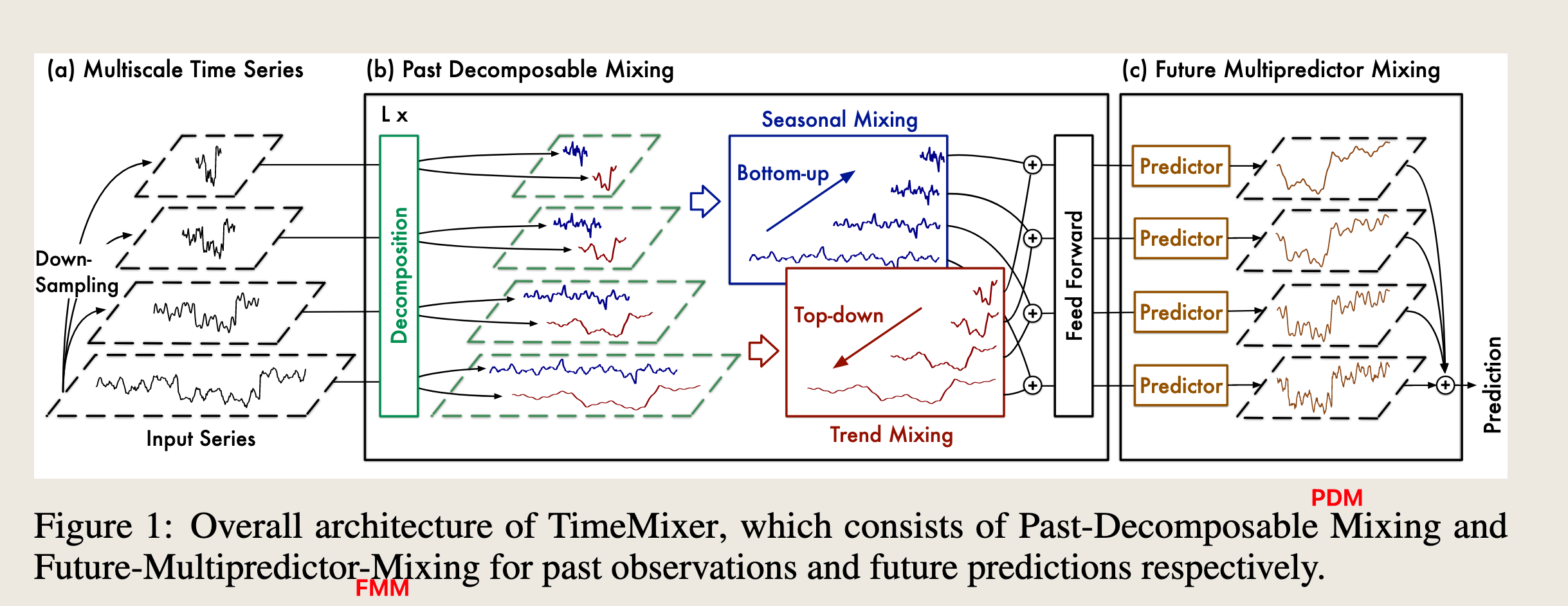
PDM(Past-Decomposable-Mixing)

==处理：== 输入上一层、输出下一层

$X^l = PDM(X^{l-1}) ,l \in \{0,...,L\}$

$L$ : 总层数

$X^l = \{x_0^l,...,x_M^l\},x_m^l\in \mathbb{R}^{{\frac{P}{2^m}}\times d_{model}}$

FMM(Future-Multipredictor-Mixing)

$\hat{x} = FMM(X^L)$

$\hat{x}$ 表示最终的预测

3.2 PAST DECOMPOSABLE MIXING

（1）

输入：$X_l$

输出：季节性成分 $S^l =\{s_0^l,...,s_M^l\}$ 趋势性成分 $T^l = \{t_0^l,...,t_m^l\}$

处理：Autoformer 的 序列分解模块

（2）PDM 第 l 层的处理

符号说明：

• Feedforward 包含两个线性层，中间是 GELU 激活函数，用于通道之间信息交互
• $S-Mix(\cdot)$ $T-Mix(\cdot)$分别表示季节性混合和趋势性混合

==（3）季节性成分混合==

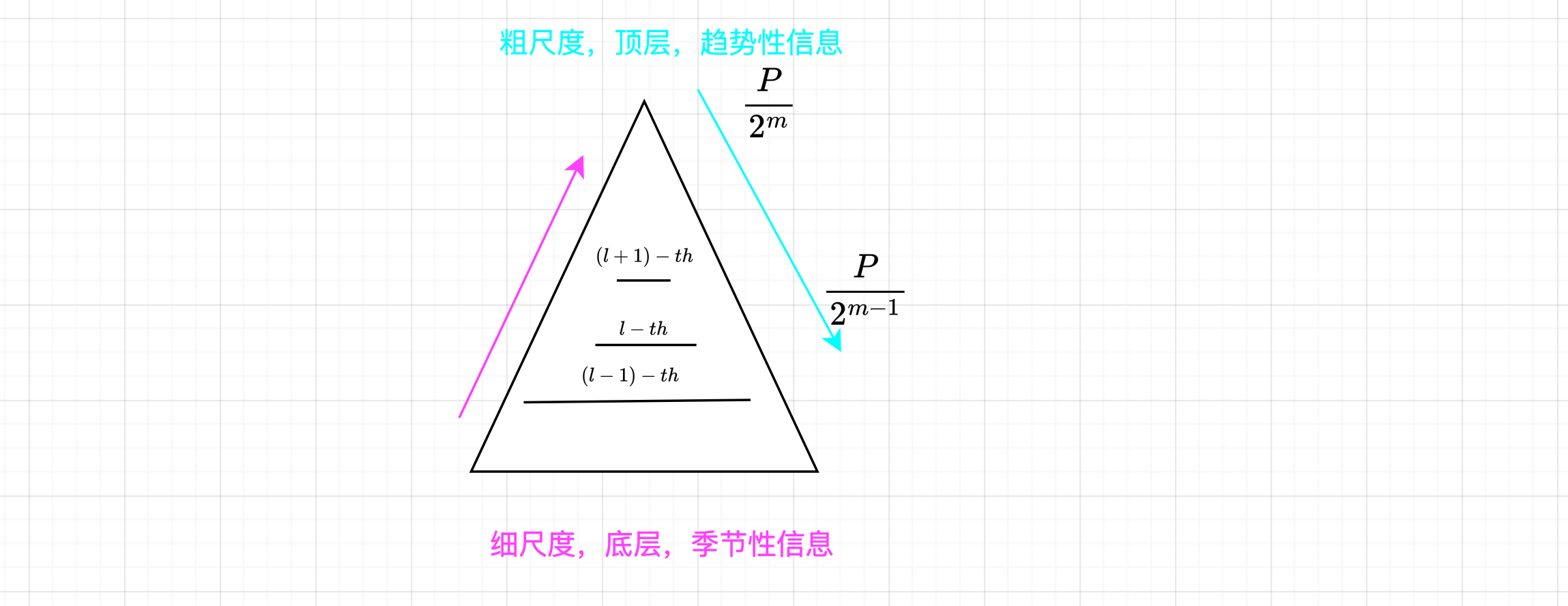
Therefore, in seasonal mixing, we adopt the ==bottom-up== approach to incorporate information from the lower-level fine-scale time series upwards, which can supplement detailed information to the seasonality modeling of coarser scales.

因此，在季节性混合中，我们采用自下而上的方法，将低层次精细尺度时间序列的信息

向上传递，这可以将详细信息补充到更粗的尺度的季节性建模中。

公式：

$s_m^l = s_m^l + \text{Bottom-Up-Mixing}(s_{m-1}^l)$

• 自底向上混合，第 $l$ 层，融入 第 $l-1$ 层的信息，用于季节性建模
• 谁是底？高分辨率？长序列？精细化？谁是上？
• 底=低层次=原时间序列=精细化时间序列
• 所以季节性混合 = 在第 $l$ 层 纳入精细化的时间序列 $m-1$
• 思想也就是：因为下采样丢失细节信息，所以补上，达到权衡
• 下采样一次，层次就高一次，粗尺度
• $\text{Bottom-Up-Mixing}(\cdot)$ 由两个线性层初始化，中间是 $\text{GELU}$ 激活函数
• 输入维度 $\frac{P}{2^{m-1}}$ ，输出维度 $\frac{P}{2^m}$

（4）趋势项混合

• Note that the upper coarse scale time series can easily provide clear macro information than the lower level.

• 高层次、粗尺度时间序列 可以轻易地捕获宏观信息

  公式：

$t_m^l = t_m^l + \text{Top-Down-Mixing}(t_{m+1}^l)$

• 与季节性成相反，对于趋势项，在捕捉宏观趋势的时候，细节的变化会引进噪声
• 注意到高层次粗尺度的时间序列可以很轻易的提供详细的宏观信息，相比于低层次来说
• 因此，我们引入了从上到下的混合方法来利用宏观信息，来自粗尺度的宏观信息来指导精细尺度的趋势建模
• 总而言之，对于多尺度趋势成分 $T^l = \{t_0^l,...,t_M^l\}$ ，我们采用自上而下的混合方式，对于第 m 个尺度，用残差连接的方式获得 自上而下的趋势信息交互
• 公式
• $\text{Top-Down-Mixing}(\cdot)$ 两层线性层，中间是 GELU 激活函数
• 输入维度 ${\frac{P}{2^{m+1}}}$ 输入粗尺度
• 输出维度 ${\frac{P}{2^{m}}}$ 输出 精细尺度 自上而下
• PDM 逐步聚合细节的趋势性成分到粗尺度，并融入 将来自粗尺度的 宏观趋势信息 作为先验知识。（对于第 $l$ 层来说，既有来自 $l-1$ 层的季节性成分，又有来自 $l+1$ 层的趋势成分）

也就是原文的图 2

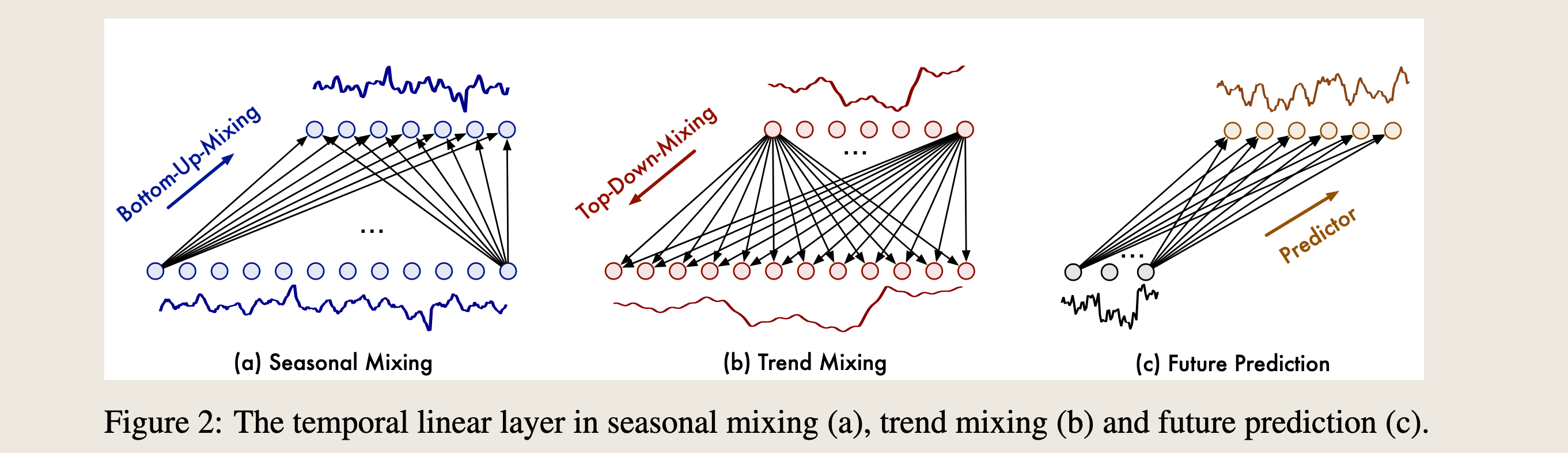
3.3 (FMM)FUTURE MULTIPREDICTOR MIXING

对于第 $l$ 层的 PDM 模块，我们会获得多尺度的历史信息，记作 ：

$X^l=\{x_0^L,...,x_M^L\},x_m^L \in \mathbb{R}^{\frac{P}{2^m}\times d_{model}}$

• 因为不同尺度的序列表示不同的主导变化？因此我们提出了 对来自不同尺度的序列进行聚合预测，记作 FMM 模块：

$\hat{x}_m =\text{Predictor}(x_m^L),m \in \{0,...,M\},\hat{x}=\sum_{m=0}^M \hat{x}_m$

符号说明：

• $\hat{x}_m \in \mathbb{R}^{F \times C}$ 表示 第 $m$ 层尺度序列的预测
• 最后的输出记作： $\hat{x}\in \mathbb{R}^{F \times C}$
• $\text{Predictor}_m(\cdot)$ 表示 第 $m$ 层尺度序列的预测器
• 首先使用单层线性层直接对未来的 $F$ 长度 的未来进行回归，从 长度$\frac{P}{2^m}$ 过去信息中提取

• 输入 $\frac{P}{2^m}$
• 输出 $F$

• 还原维度，将深层表示 $d_{model}$ 还原回 $C$

实验环境

• a single NVIDIA A100 80GB GPU
• L2 损失
• M 个尺度的划分，根据时间序列的长度进行设置

参考链接

论文精读 | 2024[ICLR]TimeMixer: 可分解多尺度融合的时间序列预测

论文研读之基于MLP的时序预测模型TimeMixer：时序分解+多尺度混合