Attention is All you need

空间注意力

开山老祖 Attention is all you need , 大名鼎鼎的transformer

什么是注意力机制

什么是注意力机制呢?

给你一张图片, 关注点肯定在于你所感兴趣的地方, 注意力机制就是让模型主动去学习您所感兴趣的,或者说是对你重要的区域和数据

发展历史

简单了解一下注意力机制的一个发展历史

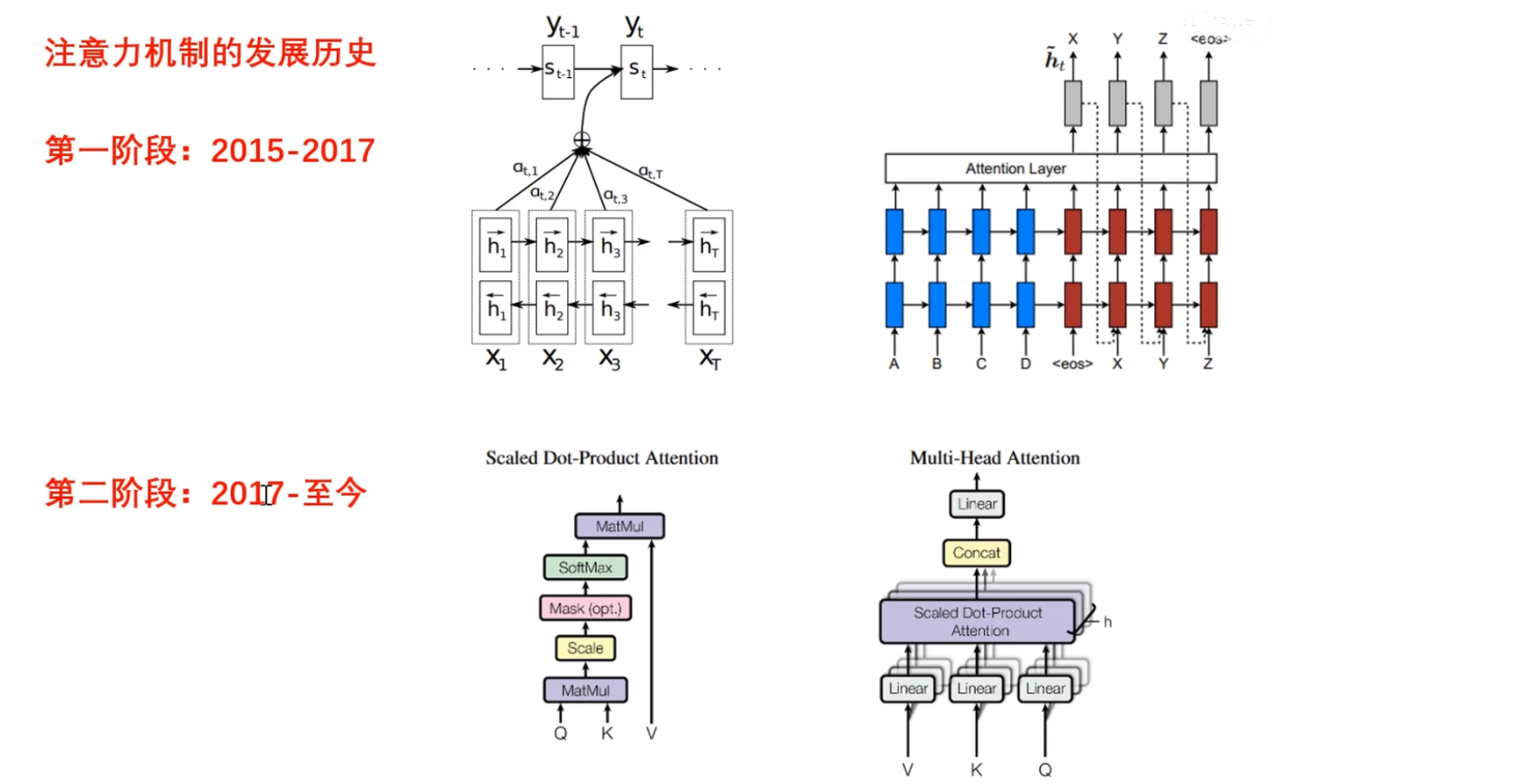
2015~2017年 , 注意力机制是在NLP任务上被率先提出的, 通常是是配合着循环神经网络一块使用,这是注意力机制的一个雏形
在2017年之后, 直到至今transformer横空出世, 重新整合了注意力机制, 相应的还设计了多头自注意力机制 , 并且将它们嵌入到了一种新的架构, 也就是transformer, transformer能够并行处理数据而无需循环操作, 这大大提升了计算效率, 直到现在依然是主流的架构

计算示例

来简单看自注意力机制的计算

有$QKV$ 3个输入,QKV 既可以是同一个表示, 也可以是不同的表示

首先, 在Q和K之间执行矩阵乘法, 得到注意力矩阵, 然后执行Scale 放缩操作, 接下来的mask, 这个操作是可选可不选的 , 然后对注意力矩阵执行softmax归一化操作, 得到0~1之间的权重表示, 然后再与V进行矩阵乘法, 相当于进行加权, 得到输出表示

▶️ 举例 : 我一进门就看见常威在打来福

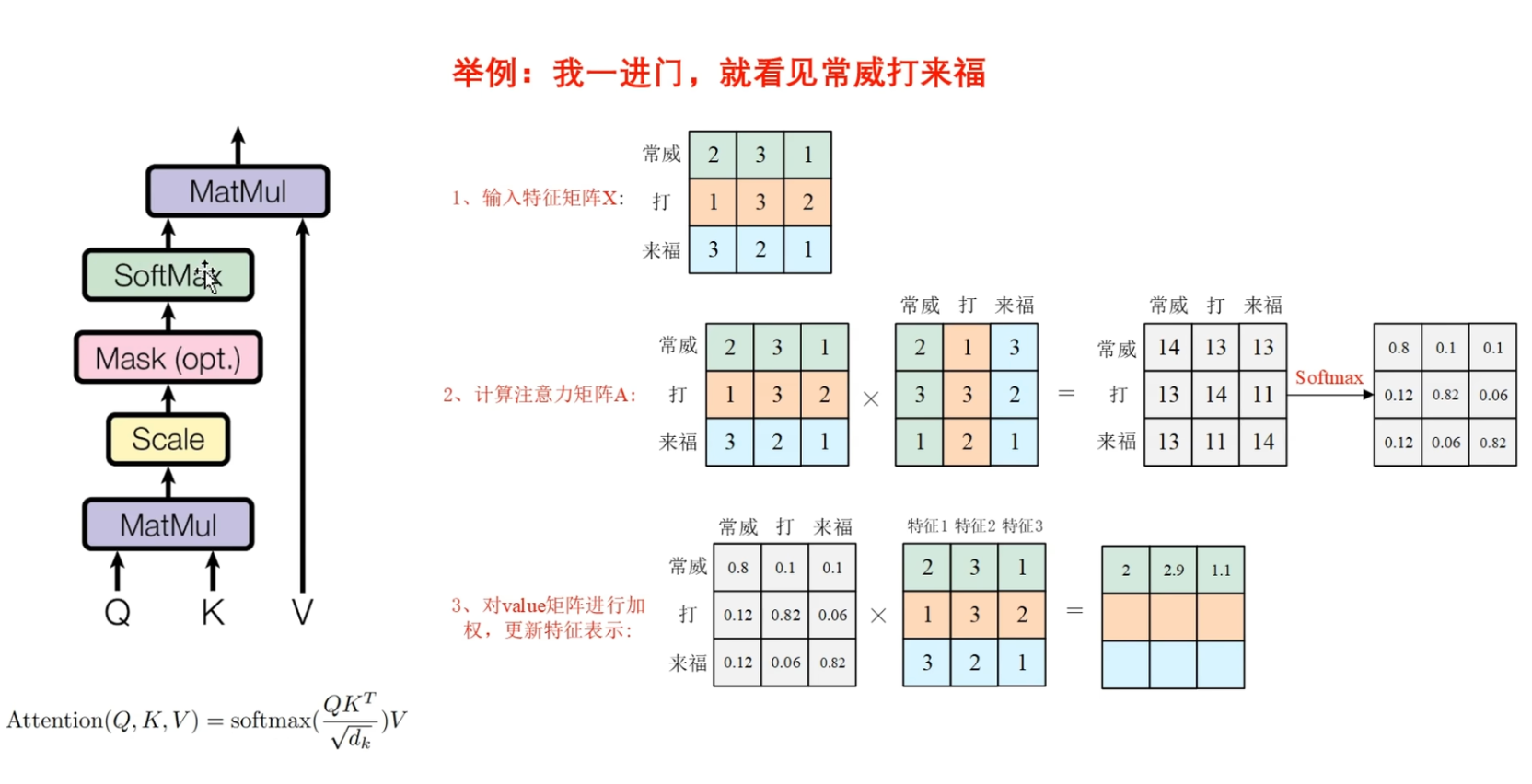
让我们来探索一下常威打来福之间的关系, 那么这个输入特征矩阵X,包含三个词向量,分别是常威, 打, 来福

我们在这里默认$QKV$都使用特征矩阵$X$

然后我们在Q和K之间进行矩阵乘法, 通过矩阵向量之间的点积, 就可以得到两两词向量之间的相似度, 例如第一行和第一列相乘, 就可以得到常威和常威之间相似度

那么通常来说, 对角线上的值一般是最大的, 因为它代表了自己和自己之间的相似度

接下来我们在这个注意力矩阵之后, 添加一个scale操作以及一个softmax操作, 将它变为0~1之间的一个权重值(例子中的权重值表示意思,理解意思即可)

当得到这个注意力矩阵之后, 与value矩阵进行相乘

例如我们将第一行权重与每个词向量的第一个特征进行相乘, 也就是第一行与第一列相乘,得到特征1的更新后的表示

同样的方式, 第一行和第二列, 第一行和第三列, 就能够得到特征2 和特征 3更新后的表示

以这样的方式, 我们就能够得到更新后的常威的一个词向量表示, 也就是第一行.

以上是基本的注意力的计算过程

关于几个问题

再来明确注意力机制中的几个关键的问题

第一个问题, QKV是怎么来的

为什么要有QKV

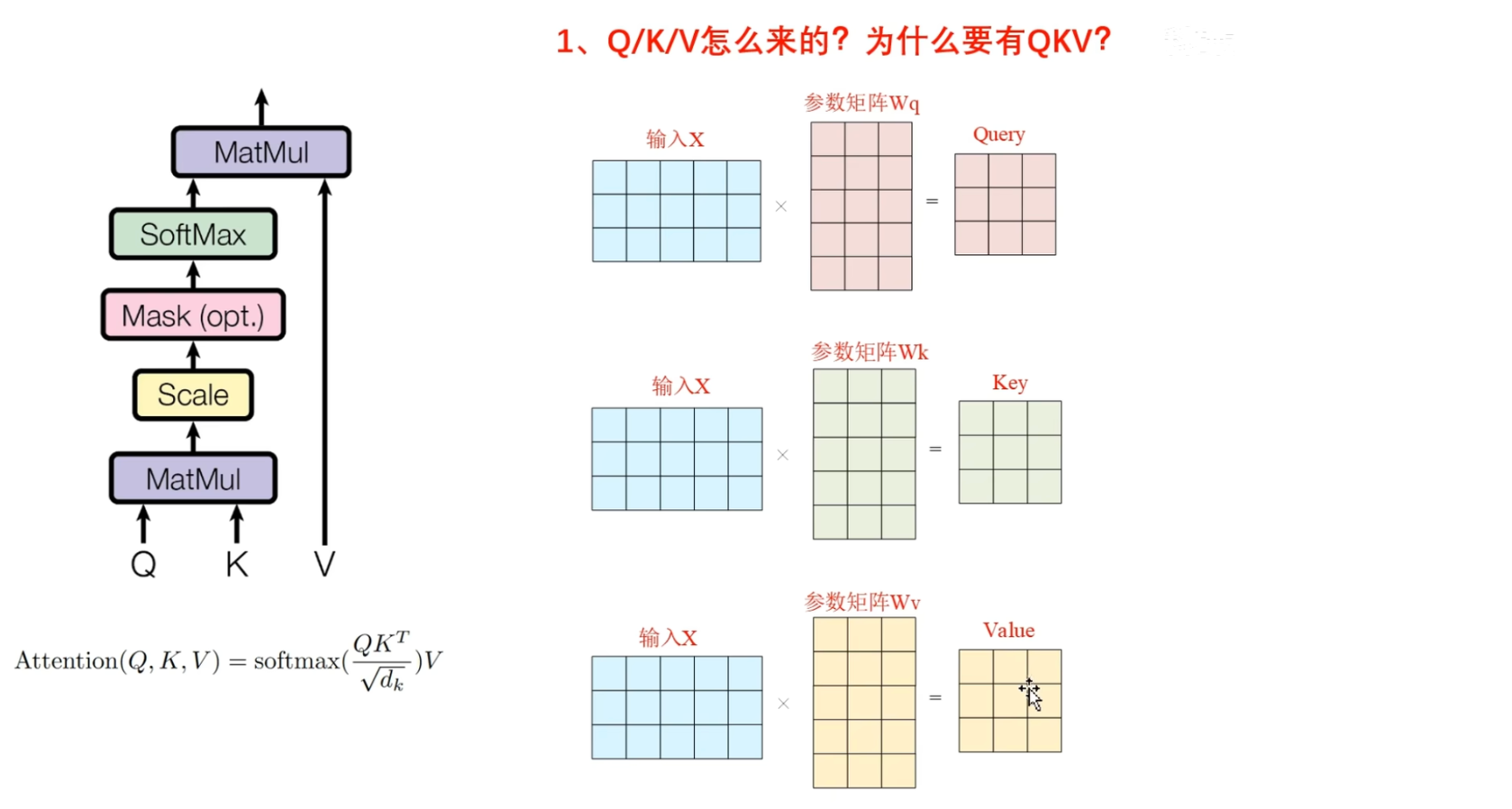
很显然, 只有一个输入X, 它通过了三个不同的全连接层第一个,第二个,第三个, 这三个全连接层具有不同的参数矩阵, 也就是 $ W_Q,W_K,W_V $

然后分别生成了$Q$矩阵,$K$矩阵和$V$矩阵

也就是 QKV矩阵是X在不同向量空间中的表示, 并且三个可学习的参数矩阵, 也能够增强模型的学习能力

非得Q,K,V3个矩阵吗?只要一个Q矩阵, 或者说只要Q和K矩阵可以吗?

回答: 可以, 只是作者证明了, QKV3个矩阵的学习能力会更强一些, 但是这并不是必须的,有可能在你的任务上, 只需要一个Q矩阵效果就已经达到最优了

第二个问题为什么要在 Q 和 K 之间做乘法?

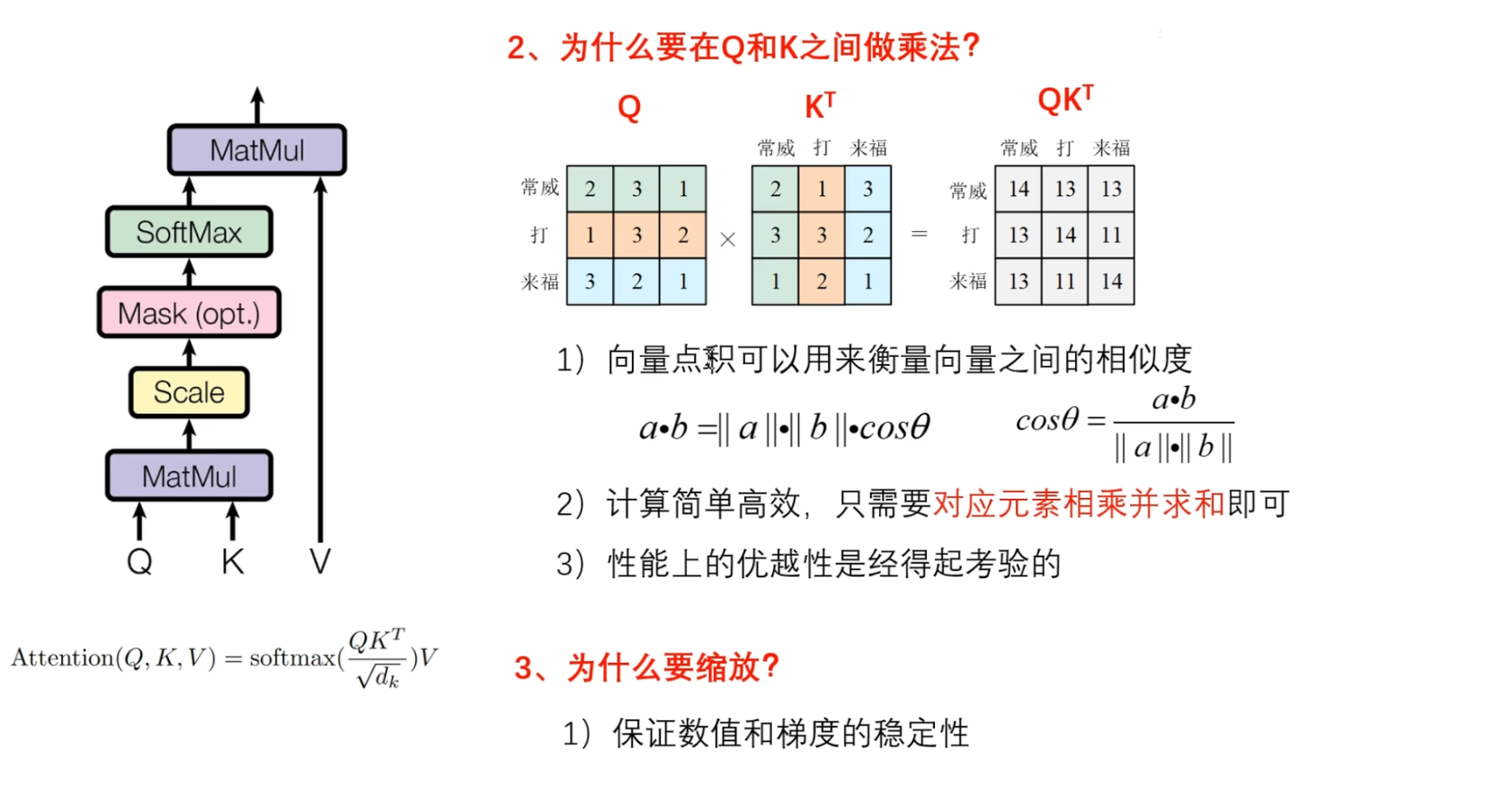首先向量乘法,也就是向量点积, 可以用来衡量向量之间的相似度

向量a和向量b的点积等于$向量a的模 × 向量b的模 × 夹角的余弦值$

当给定两个确定向量的时候, 也就是当给定一个a向量和b向量的时候, 如果它们之间的夹角越小, 那么 $\cos \theta$ 就越大, 相应的点积的值就越大, 那么如果它们的夹角越大, 那么 $\cos \theta$ 就越小, 相应的点积值就越小, 从整体上来看, 点积操作既有长度信息(模长),又有方向信息 ( $\cos \theta$ ), 就很全面

所以说, 可以用向量点积衡量向量之间的相似度

那为什么不用余弦相似度?

要计算余弦相似度, 就得求向量a和向量b的模长, 这个计算是非常耗时耗力的,但是点积的话就非常的高效, 只需要对应元素相乘并求和即可,还有,点积的操作,在性能的优越性,是完全经得起考验的, 是被成千上万篇论文验证过的

第三个问题:为什么执行缩放操作?

可以想象一下, 把向量的维度设置为64和设置为 512, 在计算点积的时候,数量级上就有差异.

很显然设计的维度越大,点积的值就越大,这样的话在计算softmax函数的时候,也就是 e 的 x 次方的时候, 你想想这可是指数函数, 当这个数值变大, e 的 x 次方就会飞速的增长, 这样就会导致梯度变得很不稳定

所以说我们在这里除以一个缩放因子,也就是 $ \sqrt{d_k} $ , $ \sqrt{d_k} $ 是向量维度的平方根, 这样做既可以保持数值上的稳定性, 也可以保持梯度上的稳定性,这就是缩放的意义所在

多头自注意力机制

多头自注意力机制就是由多个缩放点积注意力构成的, 大家各计算各的互不相干, 最后只要将每个自注意力机制的输出,进行拼接, 再通过线性层融合就可以了

这里相对比 NLP 中,[B,T,C],拆的就是 $C=h×d_h$

[B,T,C] -> [B,T,H×d]->[B×H,T,d]->[B,T,H×d]

[B,T,C] -> [B,T,H,d]->[B,H,T,d]->[B,H,T,d] query

attn.shape [B,H,T,S]->[B,T,C]

那么在这里有两个点需要注意一下:

第一个:如何划分多头?

NLP 中:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


def forward(self, q, k, v, mask=None):
    batch_size, sequence_length, model_dim = q.shape

    # [B, L, d_model] → 线性投影 → [B, L, H*d_k] → view → [B, L, H,d_k] → transpose  → [B, H, L, d_k]
    q = self.q_proj(q).view(batch_size, sequence_length, self.num_heads, self.head_dim).transpose(1, 2)
    # [B, L, d_model] → 线性投影 → [B, L, H*d_k] → view → [B, L, H,d_k] → transpose  → [B, H, L, d_k]
    k = self.k_proj(k).view(batch_size, sequence_length, self.num_heads, self.head_dim).transpose(1, 2)
    # [B, L, d_model] → 线性投影 → [B, L, H*d_v] → view → [B, L, H,d_v] → transpose  → [B, H, L, d_v]
    v = self.v_proj(v).view(batch_size, sequence_length, self.num_heads, self.head_dim).transpose(1, 2)

    # [B, H, L, d_k] × [B, H, d_k, S] → 矩阵乘法(torch.matmul) → [B, H, L, S]
    scores = torch.matmul(q, k.transpose(-1, -2)) / math.sqrt(self.head_dim)

    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e09)

    # [B, H, L, S] → softmax → [B, H, L, S]
    prob = F.softmax(scores, dim=-1)

    prob = self.dropout(prob)

    # [B, H, L, S] × [B, H, S, d_v] → 矩阵乘法(torch.matmul) → [B, H, L, d_v] → 转置(.transpose) → [B, L, H, d_v] → 重塑(.view) → [B, L, d_model]
    attn_weights = torch.matmul(prob, v).transpose(1, 2).contiguous().view(batch_size, sequence_length, model_dim)

    # 恢复原始维度：[B, L, d_model] → 线性投影 → [B, L, d_model]
    output = self.o_proj(attn_weights)
    return output

最简单的方式, 当给定一个BCHW矩阵的时候,可以在这个通道C上平均划分为为$M$组,每组的通道数量是K, $M×K=C$

为了便于计算,通常会将M迁移到第一个维度上面, 然后让它重新变为一个4维矩阵, 这样的话每一组的计算都是独立的, 那么第二个点在输出的时候,我们将多个头的输出在通道上进行拼接, 并且恢复和输入相同的shape, 然后再通过线性层

在这里这个拼接和这个线性层该怎么理解呢?

首先,多头自注意力机制每一个头都在不同的向量空间进行计算, 在不同的向量空间提取有用的特征

举个例子,我们要提取一个人的特征,多头自注意力机制就可以看作是在不同的头分别关注身高年龄长相工作等特征,最后将这些不同向量空间的特征进行拼接,然后再通过一个线性层进行融合,得到更新后的特征,这就是多头自注意力机制

是,已经被讲的太多太多了,但每次看还是有新的体会