COT上下文 transformer网络

CVPR2021,扩展版本发表在TPAMI2022

简介

大多数现有的设计直接在2D特征图上应用自注意力机制,以获取基于每个空间位置的孤立QK对的注意力矩阵,但没有充分利用K周围的丰富上下文信息

动机

注意力机制在两两像素之间计算相关性, 这可能会错误的分配注意力权重,所以作者设计了一种上下文transformer网络(COT),充分利用了K的上下文信息来学习动态的注意力矩阵,这能够有效的增强模型的表征能力

说到底,还是利用了上下文信息,也就是说现在不是独立位置的QK对,而是独立的Q和具有上下文信息的K来计算相似性

案例图

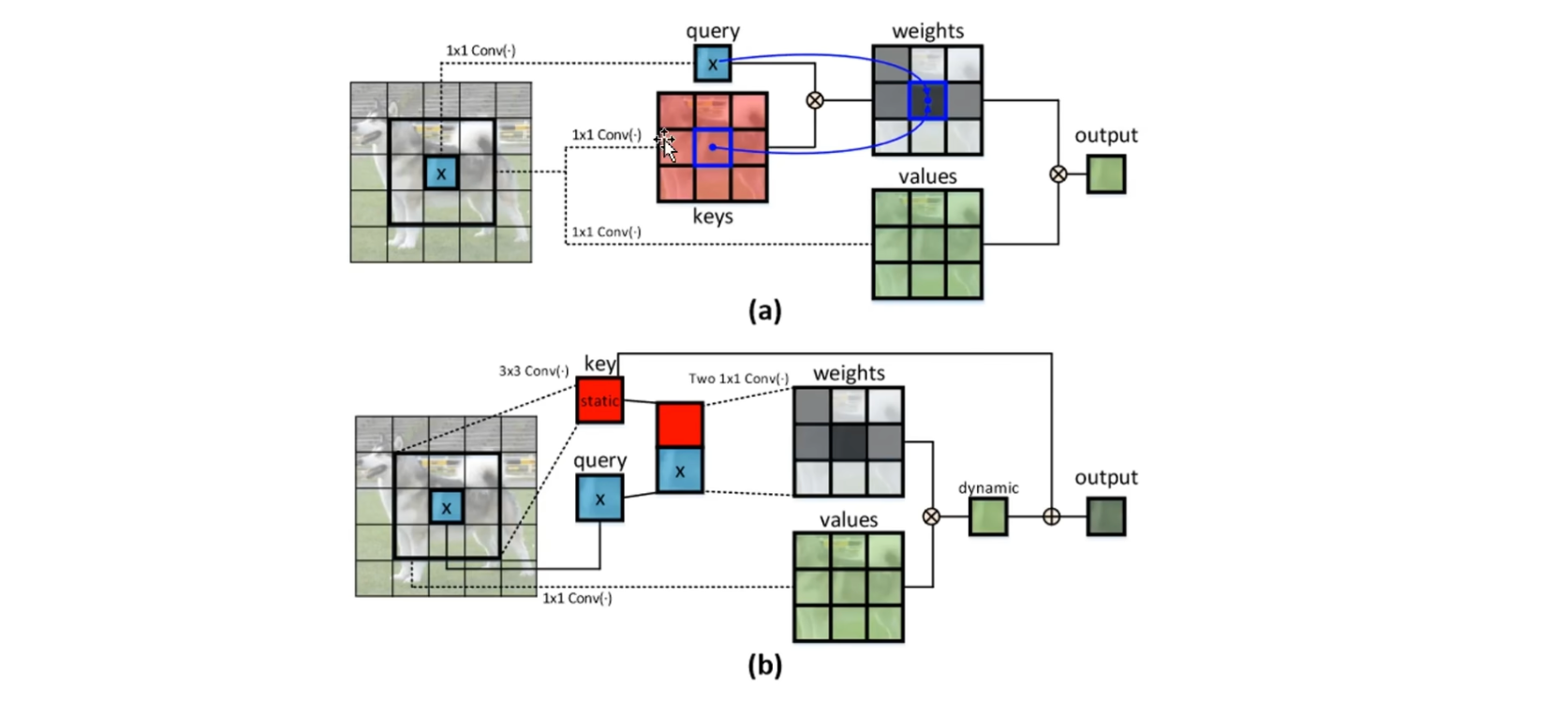
上面的图是传统的注意力机制,首先$QKV$分别通过$1×1$的卷积层得到,这里是一个像素点$X$来作为query, 使用$3×3$大小的像素点窗口,来分别作为K和Value,这里的注意力矩阵是通过像素点 Q和K中的所有像素点依次进行向量点积,来得到权重矩阵

例如这个像素点query(x)和K矩阵中间的像素点进行点积,得到的就是对应权重矩阵中的中间像素位置权重,然后将得到的注意力矩阵,与value矩阵进行矩阵乘法,就可以得到$X$元素更新后的输出

作者的动机主要是在注意力矩阵,认为这种互不干扰的点积不太可以,因为没有考虑到周围的上下文信息,都是独立来计算的,这样可能就会错误的得到权重

🟢 下面的图是 COT 网络

可以看到这里的 query,也就是像素 X,并没有通过1×1的卷积变换,用的就是原始的X的特征表示

K矩阵,依然是3×3大小的像素点窗口,但不同的是它执行了一个3×3的卷积,得到了一个局部上下文向量K,然后,将这个query和这个K向量,在通道上进行拼接,然后通过两个1×1的卷积进行变换,得到了权重矩阵

接着这个权重矩阵与Value矩阵进行加权,得到动态上下文表示

最后动态上下文表示,和之前的静态的K信息进行拼接,相加得到最后的输出

思考: 一个拼接后的向量,怎么就能变成注意力权重矩阵呢?(见后)

计算流程图

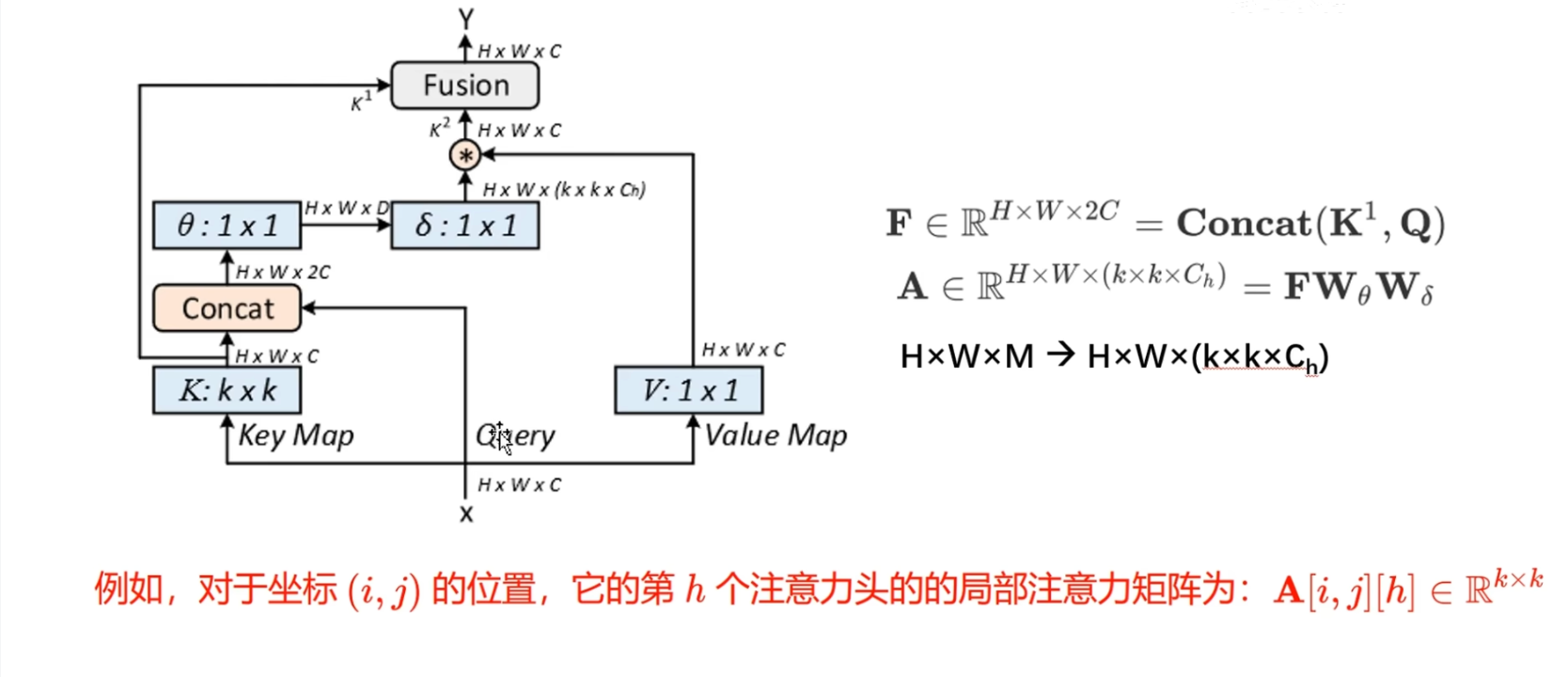
直观的看上去感觉很简单

让我们仔细来看一看,首先这个Q矩阵没有通过线性层变换,还是原始的输入X

K矩阵,是通过$K×K$的卷积层来得到的,输出是$H×W×C$ , 在这里要注意一下, 目前的K矩阵通过卷积操作提取了每个像素点的周围信息,是一个静态矩阵,这个静态矩阵在后面需要用得到

继续看K矩阵和query的矩阵在通道上进行拼接,得到的是 $H×W×2C$ 的矩阵表示,然后通过两个1×1的卷积

首先通过第一个1×1卷积,得到的是$H×W×D$的特征表示, 很显然1×1的卷积层的权重矩阵是$2C×D$ , 然后进行第二个$1×1$的卷积层 , 通过了之后,维度就变成了 $H×W×(k×k×C_h)$

why?

首先要明白 $(k×k×C_h)$ 乘积的结果还是代表通道的数量

如果不好理解,可以先写成 $H×W×M$

先理解成 $H×W×M$的形式

写成这个形式的话,我们就看不出来 这是一个代表像素对之间的权重矩阵,形式上就是一个简单的特征表示

分析,因为 $H×W$ 代表的是像素点的总数, 这是不变的

接下来分析 通道 M,这里作者将通道 M 变成了 $k×k×C_h $

🟢 那么为什么要变成 $k×k×C_h$ ?

这里要回到作者的动机,作者觉得每个独立的QK对的注意力矩阵是不合适的,因为没有考虑到上下文信息,所以在这里,作者考虑了key的上下文信息,具体来说,对K执行了$3×3$的卷积,得到的局部上下文表示,那这样的话每个query,对应的就是 $K×K$ 的像素点, 对应的每个K都包含了 $K×K$ 的像素点的信息

那怎么理解 $C_h$ ?

类比 多头注意力机制, 多个头在不同的向量空间独立计算,能够获取更多种类的信息,作者在这里也考虑了这个角度, $C_h$ 就是头的个数, 相当于对于每个query像素来说, 都有 $C_h$ 的注意力矩阵, 每一个注意力矩阵的shape 都是$K×K$

另理解:

对于坐标$ij$的位置或者像素点来说,它的第 $h$ 个头的局部注意力矩阵为 $A[i,j][h] \in \mathbb{R}^{k × k}$ , 是一个$K×K$的矩阵表示 , 最后我们将得到的注意力权重矩阵,与value矩阵进行加权, 得到一个动态上下文表示

最终的输出就是 动态上下文表示 和 静态上下文信息K 的融合

📝 启示:

深度学习具有很大的开放性, 很多东西只要能够解释得通, 并且具有一定的性能,那么它就是具有创新性的

比如这篇论文中, 为什么一个$1×1$卷积能够学习到像素点之间的权重表示? 这里的理解是, 神经网络可以拟合任何函数, 只要定义它是权重矩阵, 那它就是权重矩阵, 但是任意变化的前提下是整个逻辑说得通, 维度对得上