ECA Net 有效的通道注意力

ECA Net有效的通道注意力

CVP2020

简介

现有的通道注意力方法,尽管提高了性能,但不可避免地增加了模型的复杂性

从计算复杂度入手,克服性能和复杂度之间的矛盾,为此,本文提出了有效的通道注意力模块,该模块只涉及少量参数,同时具有明显的性能增益

通常来说,大力出奇迹,模型在某个范围内不断的上强度,是有利于性能提高的

emmm……持保留意见

作者认为降维会对通道注意力预测产生副作用,并且捕捉所有通道的依赖关系是低效和不必要的,因此避免降维对于学习通道注意力是重要的

适当的跨通道交互可以保持性能,也能显著降低模型复杂性

总结动机:

第一点,降维有副作用

第二点,通道之间的交互,不用全部都交互

因此提出了一种不降维的局部跨通道交互策略

该策略可以通过1D卷积有效的来实现,作者直接使用的一个1D卷积进行实现

基于此,作者做了实验,验证这个想法

(1)不降维

(2)局部跨通道交互

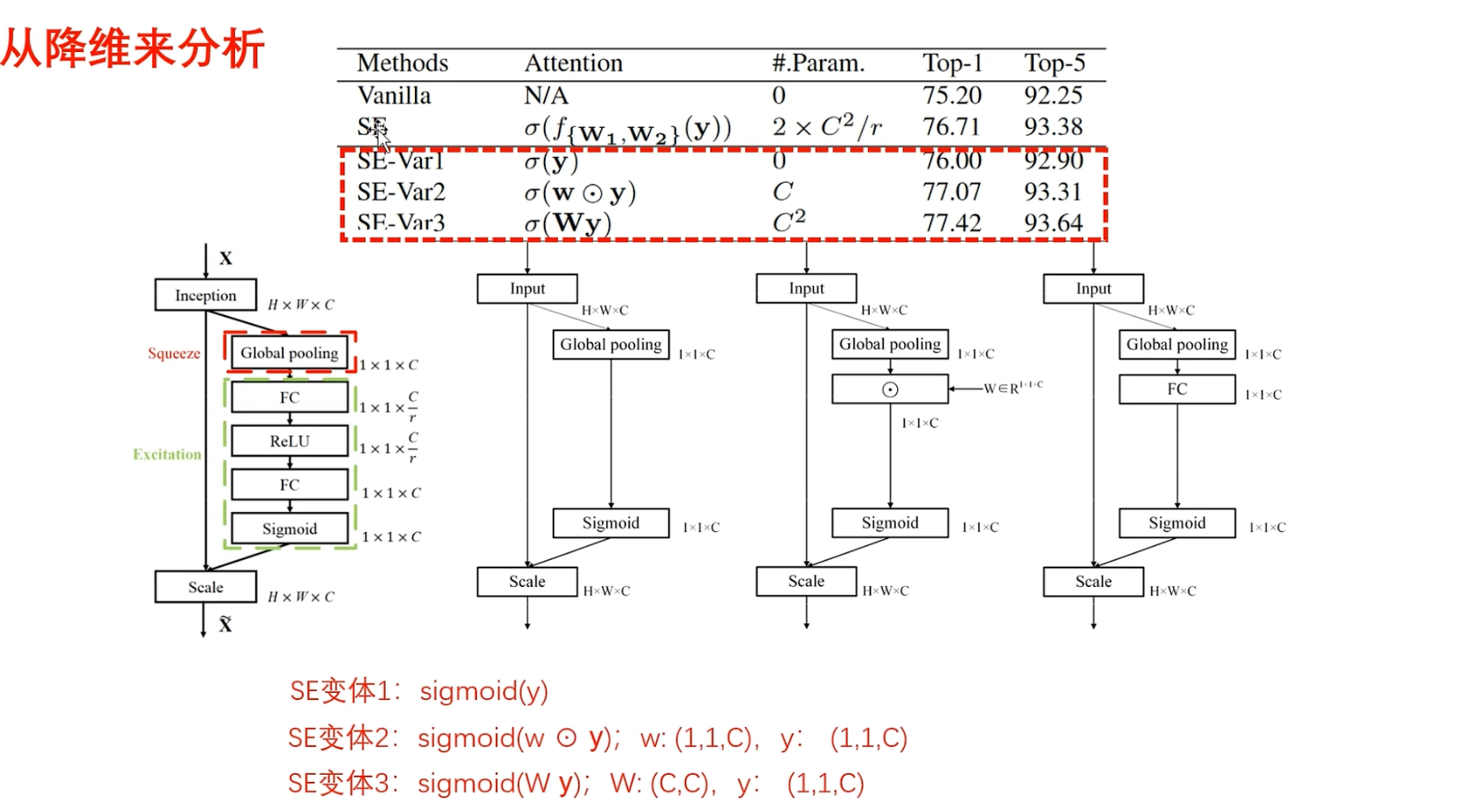
看作者的实验内容

(Vanilla)第一个:原始的网络ResNet
(SE)第二个是添加了原始的通道注意力的ResNet,添加通道注意力之后,性能提高,说明通道注意力的有效性
(SE-Var1)第三个,变的是激励部分(FC-ReLU-FC),作者干脆就没有建立通道间的依赖性,也就是说池化完成之后,直接通过Sigmoid函数来生成权重(对应第二个计算流程图,所以说参数量为 0)
(SE-Var2)(对应第三个计算流程图)池化以后,输出与一个权重进行哈德玛乘积(也就是执行对应点相乘)

这里的理解:

相当于为每一个通道都单独给一个权重,然后进行更新,这里的参数量是C,就只有C的参数

这里进一步的理解:对应点相乘,也就是说大家各乘各的,和建立通道间相关性半毛钱关系都没有

接下来分析实验性能:

首先,这三个变体都没有执行降维策略

第一个变体的性能稍微差一些,比不过SENet,但是还是比原始的ResNet网络更强一些
第二个变体是独立学习每个通道的权重,参数量只有C的参数,在涉及更少参数的情况下,性能反而优于SENet,这里意味着比起降维来说,通道和权重一一对应的关系,要更好一些,甚至不需要考虑通道间的依赖性,只要不降维,性能就不会差
第三个变体是一层的全连接,比两层且带有降维操作的,SENet的性能要更好,它的性能是最好的

通过对三个变体进行分析,可以得到结论:不降维是有效的,性能会提高

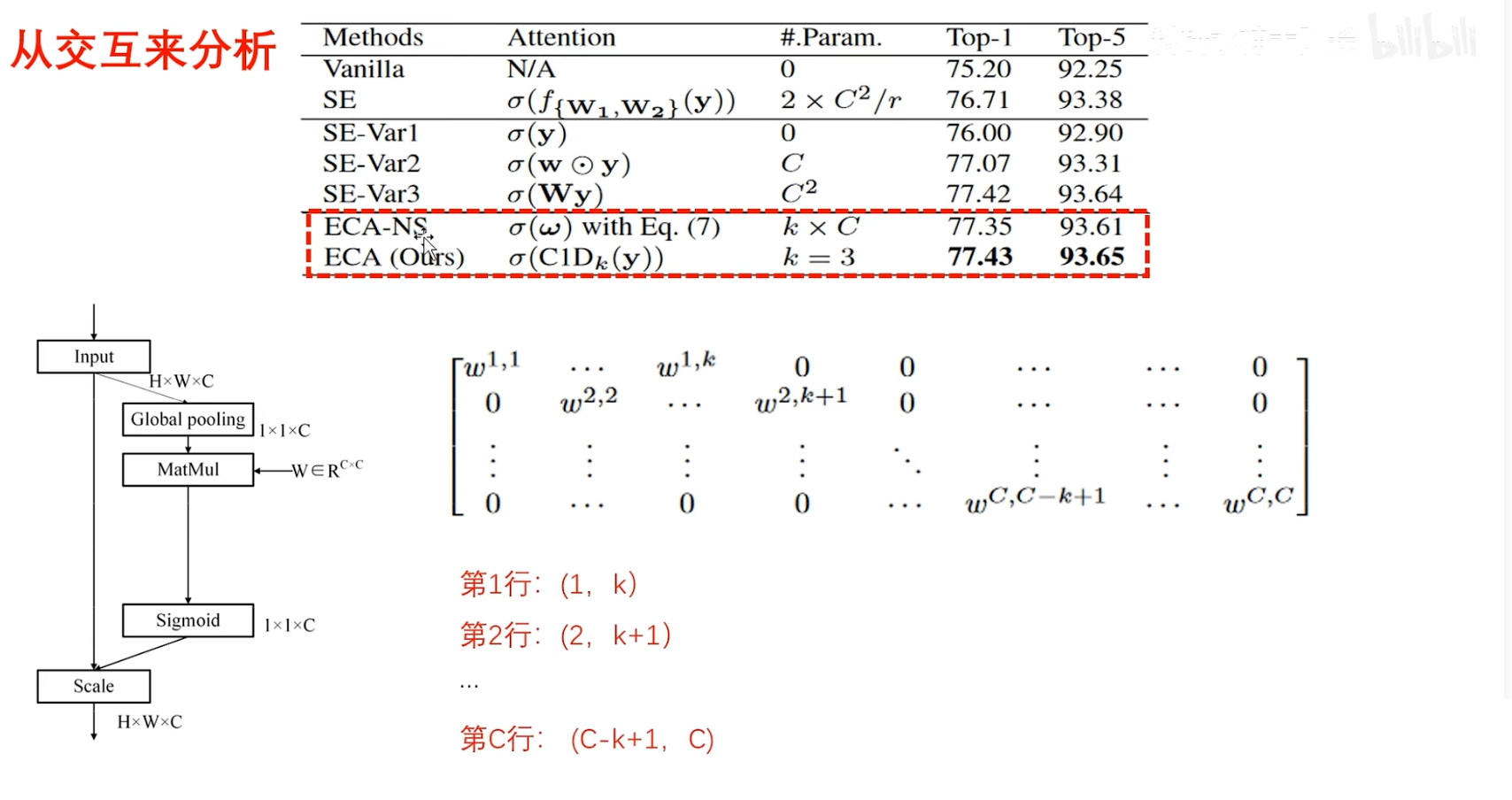
再次进行深入分析:

(ECA-NS)全局池化以后,与参数矩阵W进行矩阵乘法,本质上也是一层全连接,在分析不降维的时候,一层全连接,也就是(SE-Var3),是三个变体中性能最好的,因为它没有降维,并且在所有通道之间还进行交互了,但是,虽然性能是最好的,参数量也是最多的,$C^2$,当这个通道数量很大的时候,计算复杂度太高了,基于此,作者在这里又改进了:

为了减少参数量,并且还想在所有通道之间进行交互,也就是一个 W 矩阵,不再是一个全是参数的矩阵了,而是在参数的每一行都保留了 K 个值,其余设置为 0

此时,这个参数矩阵 W 和通道描述符( $ 1×1×C$ ) 进行矩阵乘法时,第1行就能够建立 K 个通道之间的相关性,第二行就能够建立第2个通道到第 K+1 个通道之间的依赖性,直到最后一行,就能够建立最后k个通道之间的依赖性

这里只需要$K×C$个参数,每一行是K个,总共有 C 行,又进一步降低了参数量,性能稍微略微降低了一点点,不过倒也不影响

仔细分析这里的操作,和卷积十分类似,无非卷积是共享参数,而这个W矩阵不共享参数罢了,思想是一模一样的,因此,作者尝试了 1D 卷积的效果,也就是 ECA-Net,结果发现性能是最好的,并且参数只需要 K 个

到这里为止,作者真正得到了属于自己的结论:

作者只用了一个 1D 卷积,而且卷积核只需要设置为3,性能就是最好的

在实际应用中,卷积核大小应该设置为多少,可以在自己的任务上尝试一下

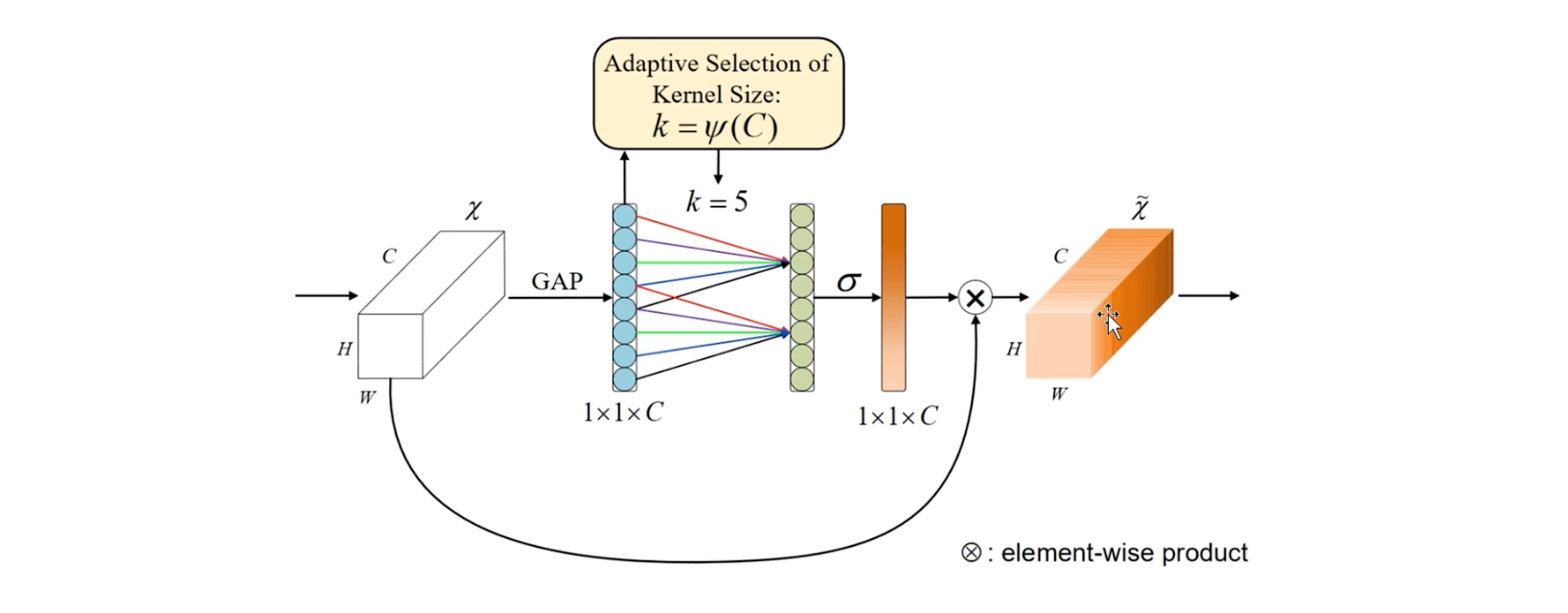
通过简简单单的池化操作,生成通道描述符表示,然后再通过1D卷积建模局部通道之间一个相关性,然后再通过Sigmoid函数生成权重,来调整输入的特定维度,得到一个输出

这一篇论文很简单,但是作者分析的非常的深入

for us

在实验过程中,也不要再盲目的在整个网络全部都使用全连接,可以尝试多在通道上应用卷积操作