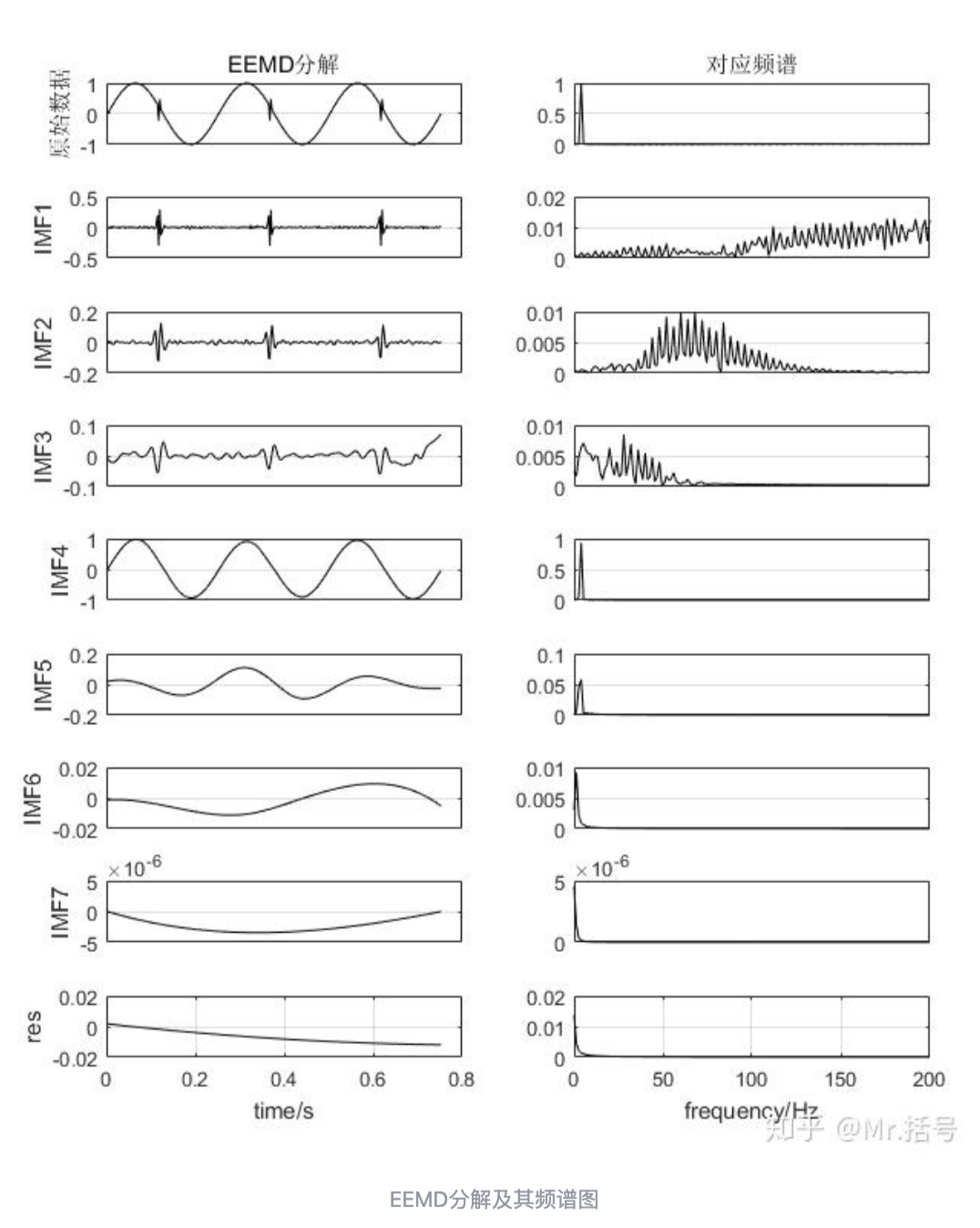
EEMD

• 把一个信号写成一系列的子信号的组合，然后加上一个性质不同的信号，所谓的残差信号或者剩余信号
• 为什么?

解决模态混叠问题

• 什么是模态混叠?

• 不同模态的信号混叠在一起

  具体来说:

① 不同特征尺度的信号在同一个 IMF 分量中出现

② 统一尺度特征的信号被分散到不同的 IMF 分量中

• HOW? 怎么解决的?

利用白噪声均值为 0 的特性,通过在分解的过程中多次引入均匀分布的白噪声,将信号本身的噪声通过多次人为添加的噪声掩盖过去,从而得到更加准确的上下包络线,同时对分解结果进行平均处理,平均处理的次数越多,噪声给分解带来的影响就越小

• WHAT? 具体怎么做的?

① 设定原始信号的处理次数 $m$

② 给这 m 个信号分别添加随机白噪声,组成一系列的新信号

③ 对着一系列的新信号分别进行 EMD 分解,得到一系列的 IMF 分量

④ 对相应模态的 IMF 分量分别求均值,得到 EEMD 分解结果

• 计算流程图

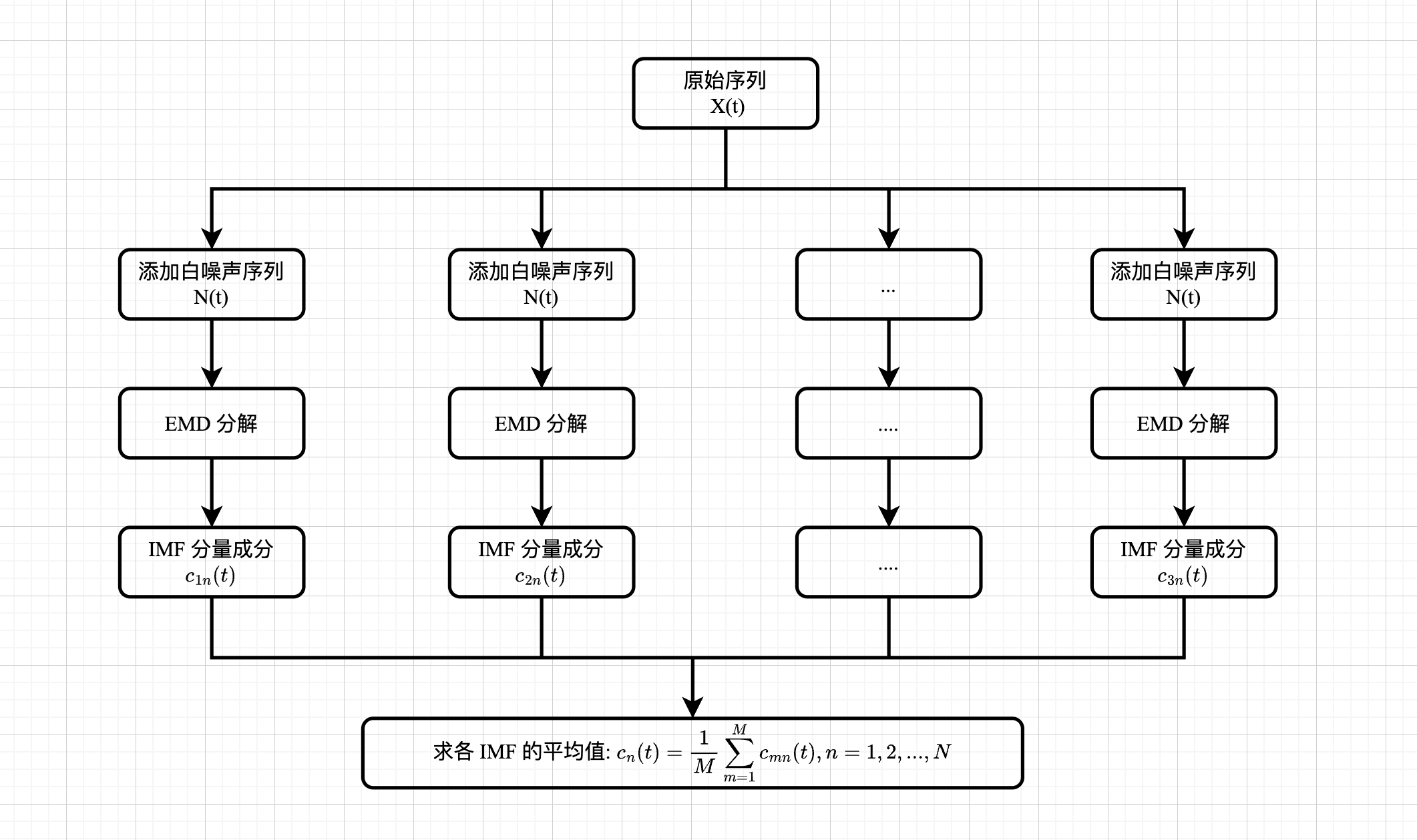
• 注意:

① EMD 无参数,自适应傻瓜式分解

②EEMD 需要调参 :

• 平均处理的次数 $m$
• 添加白噪声的幅值: 白噪声的幅值 通常用 “白噪声幅值的标准差与原始信号幅值标准差之比” 表征

例子

设有混合信号:

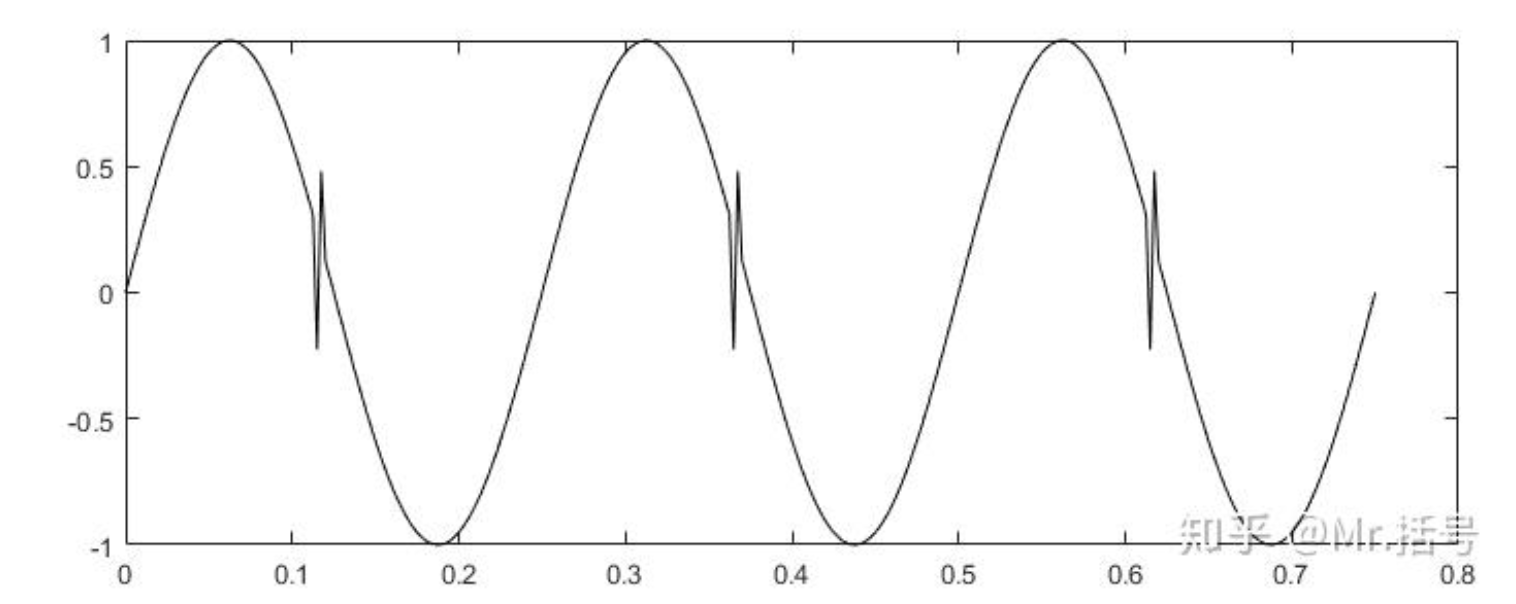
对其进行 EMD 分解:

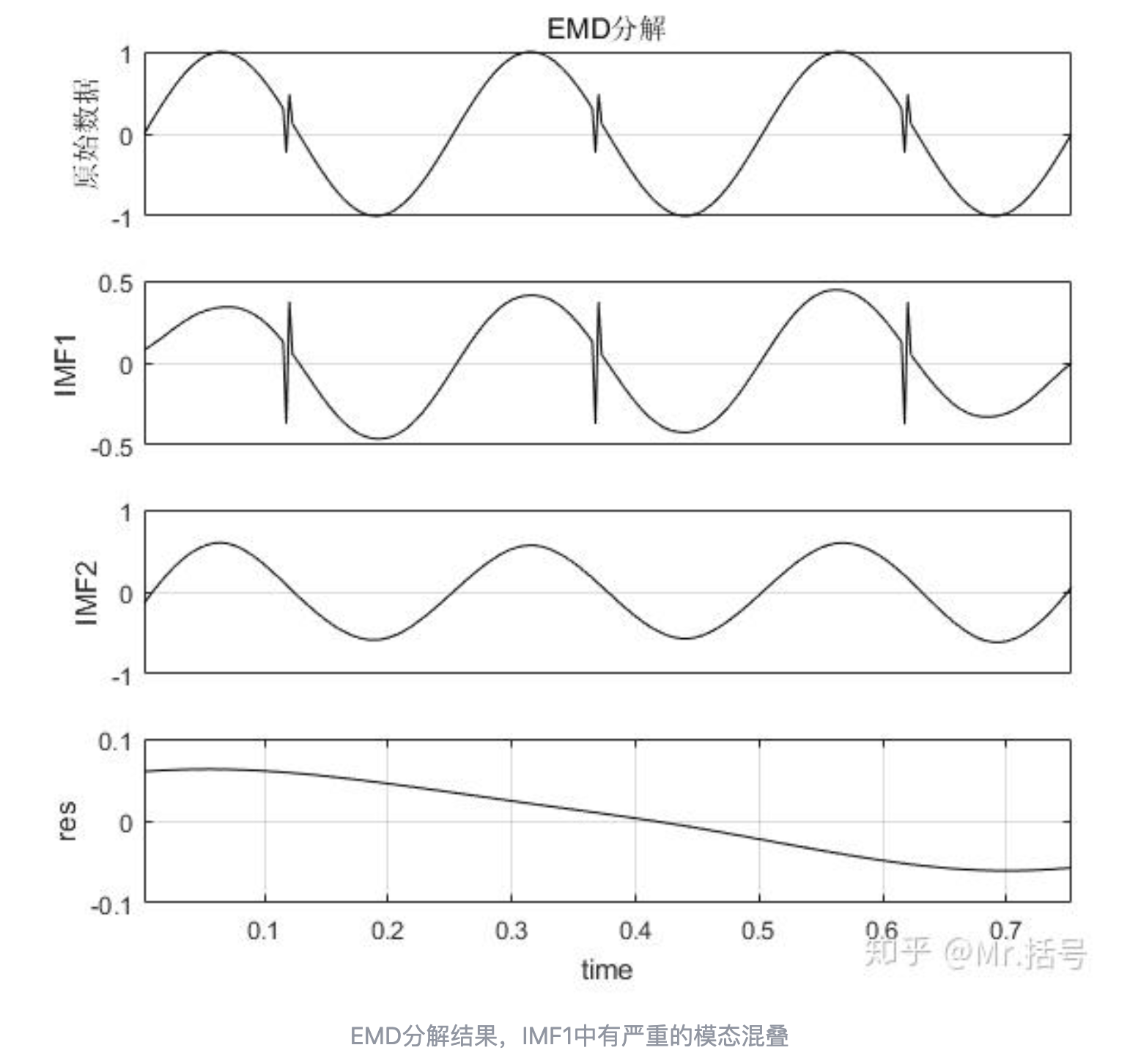
EEMD 分解:

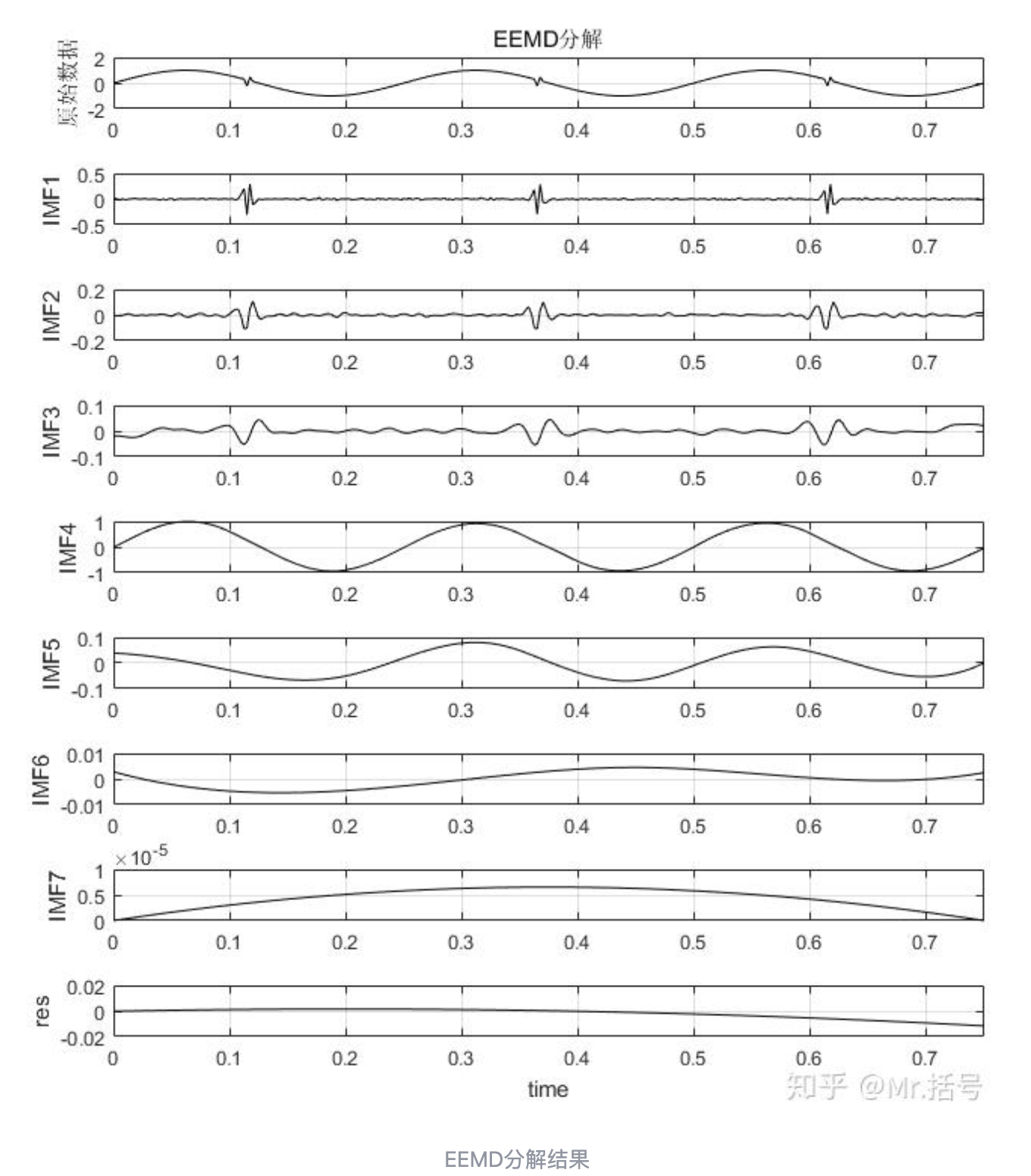
评价两种分解结果

• EEMD分解的IMF1、IMF2和IMF3是含有高频的正弦间歇性信号，IMF2和IMF3可以看做IMF1很小的能量损失，分析高频信号时，可以将IMF1、2、3叠加起来作为重构的高频信号，会得到更好的分析效果。IMF4也很好地提取了信号中的低频分量。

• 相比之下，EMD的分解结果存在着严重的模态混叠，失去使用的意义了。

❓ 还是不明白什么是模态混叠

对于有些应用场景，还需要对各imf分量的频谱进行分析，就需要如下这样的图：