有效的多尺度注意力模块
ICASSP2023
简介
利用通道降维建模通道之间的关系会带来副作用,因此,作者提出了一种高效的多尺度注意力模块
首先指出 SENet 中存在的问题: SENet通过两层全连接层来建模通道相关性,先降维后升维
之前的 ECANet已经证明了先降维后升维,会破坏通道和权重的一一对应的关系
作者提出的多尺度注意力模块和通道方面的建模是存在一定关系的
为了保持每个通道的信息和减少计算开销,作者将部分通道重塑为batch维度, 并将通道维度分组为多个子特征,使空间语义特征在每个特征组内均匀的分布
作者的做法是把通道进行分组,有点类似于多头注意力
比如说有一个1×64的向量,把它分为八组,那么每一组都是一个1×8的向量
分组的意义就是能够使空间语义特征,能够在每个组内的进行一个均匀的分布
具体而言,除了对全局信息进行编码,来校准每个并行分支中的通道方向权重之外
两个并行分支的输出特征,还通过跨维度交互进一步聚合,以捕捉像素级别的成对关系
这里作者做了两个任务
(1)第一个就是先调整通道的重要性
(2)第二个任务就是对不同尺度的输出进行交互
论文模型图
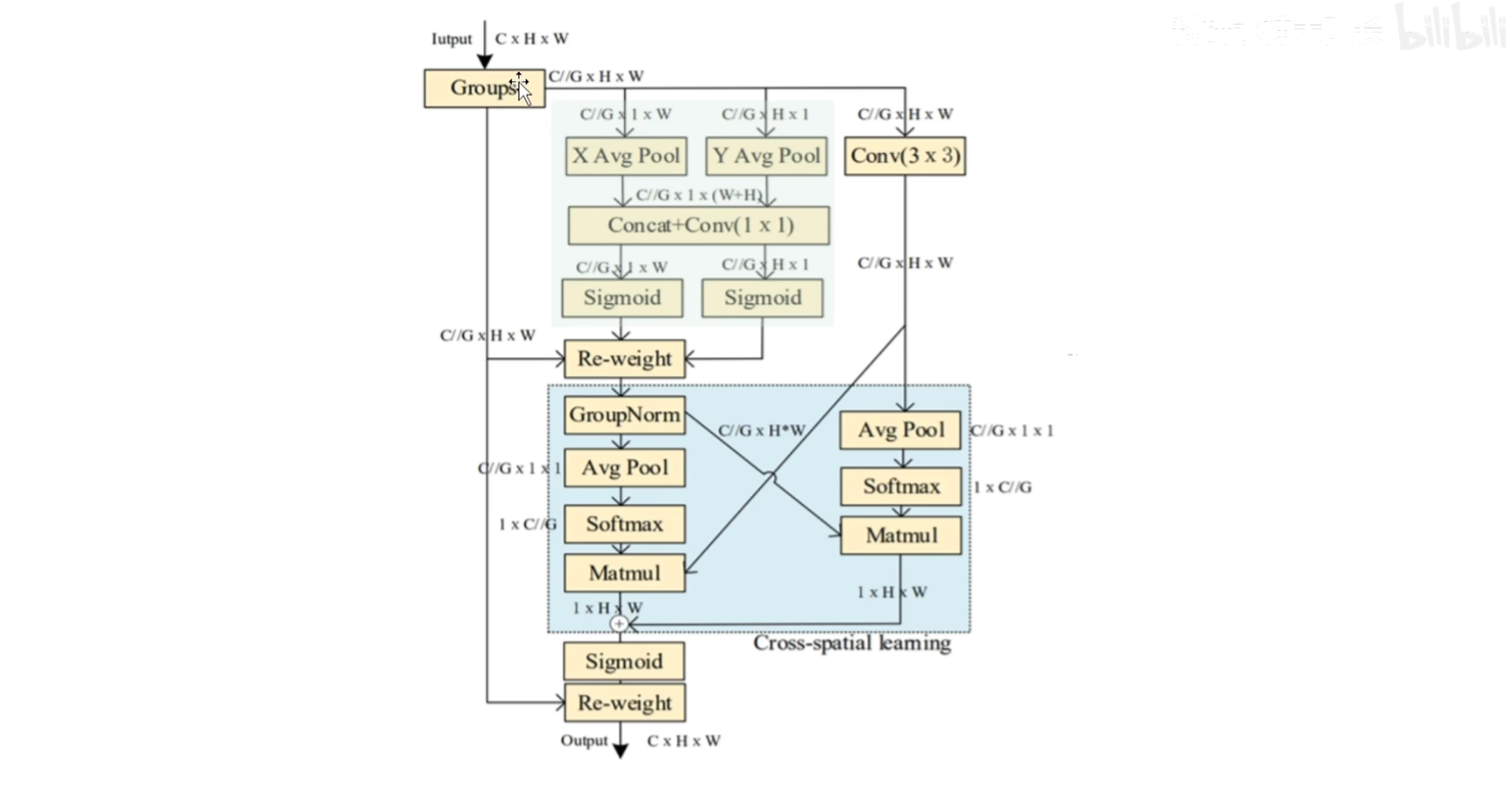
输入特征的shape是HWC
首先将C的通道分为G组,那么每一组的通道数就是 $ \frac{C}{G} $ , 然后对着这G 个组的特征进行并行计算, 这里是主要的计算模块
计算流程图
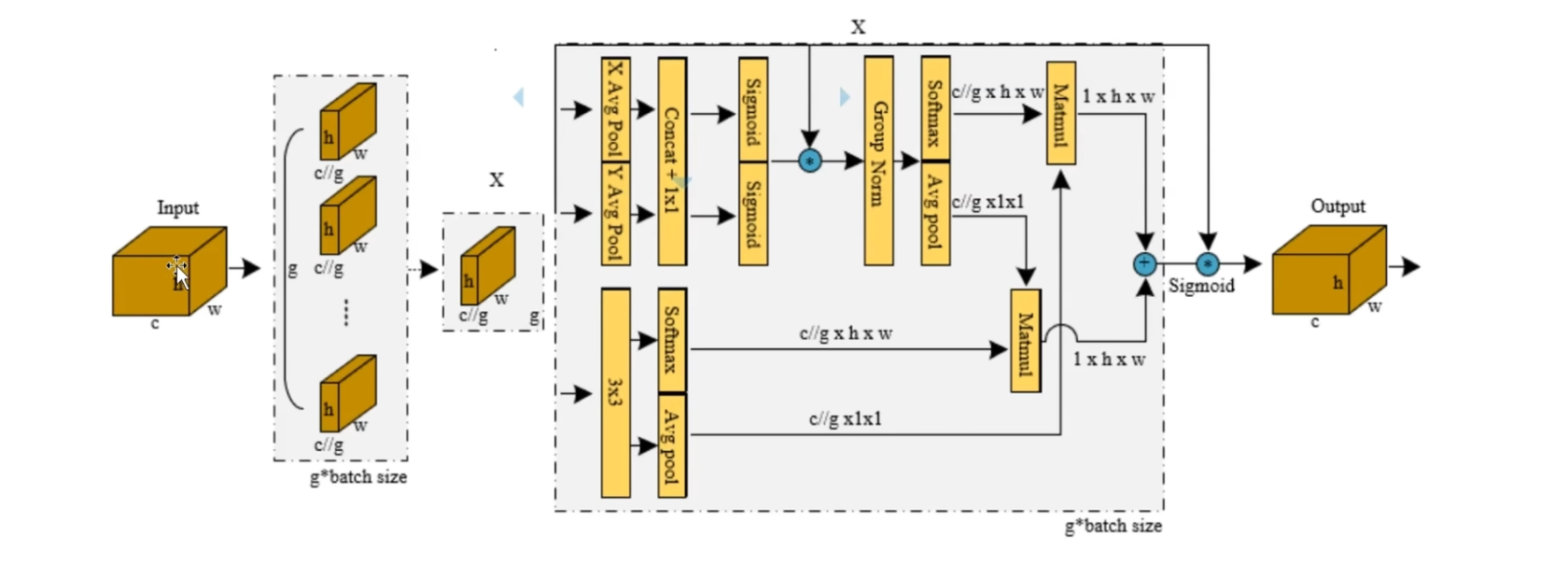
首先输入是CHW, 在通道方向上进行一个分组, 每组的shape都是$ \frac{C}{G}×H×W $, 在这里省略掉了batch维度
然后可以看到,这里有三个分支
熟悉:这前两条分支和坐标注意力, 基本上就是一模一样的
回顾坐标注意力
也就是左边的两个分支
首先在H方向上, 执行一个平均池化操作, 得到H方向上的全局依赖性,得到的 shape 就是 $\frac{C}{G}×1×W$ ,以这样的方式 , 不仅捕捉了H方向上的全局依赖性, 还能够保留$W$方向上的位置关系,因为$W$的大小是不变的
同理,在这个W方向上的操作也是同样的道理, 既能捕捉这个W和方向上的全局依赖性, 同时还能够保留H方向上的位置关系
然后将这两个分别具有H方向和W方向的全局依赖性的表示进行拼接,在这个空间维度上进行拼接,并且通过1×1的卷积来融合通道特征表示,然后再重新进行分割, 并且分别通过Sigmoid函数来生成权重表示
这样的话,就能够通过横纵坐标来准确定位图片中的具体像素点
这一块它唯一原始的坐标注意力不同的就是,在这里并没有通过线性层先进行降维后升维,而是仅仅通过1×1的卷积来融合通道特征(借鉴 ECANet 的思想)
左边的两个分支相当于是对图片中每个像素点的所有通道都进行调整了,但是没有考虑到空间信息,因为在这里每个像素点都是独立的,所以说我们可以把它看作是1×1的空间尺度(那不就是通道注意力啦?继续看后面)
为了弥补单一空间尺度的不足,也就是1×1空间尺度的不足,作者还提出了多尺度的空间建模,也就是在右边这个分支,通过了一个3×3的卷积层,来提取每个像素点的上下文信息表示
到目前为止,我们拥有了两部分的特征表示,一部分就是左分支,它有1×1尺度的输出,另外一个分支是3×3尺度的输出
作者这里很值得注意!
作者这里并没有用以往那种融合的策略,比如什么相加拼接等,作者这里提出了一个交互策略,在不同的尺度空间进行 信息聚合
🟢 信息聚合
首先看左边这个1×1尺度分支的输出,首先通过一个正则化,然后在 $H×W$ 方向上执行池化操作,得到通道描述符,通道描述符的 shape 是 $\frac{C}{G}×1×1$ , 编码了全局的空间信息, 然后执行softmax归一化,最后将归一化后的通道描述符,与3×3尺度的输出进行相乘
🚩 这里是矩阵乘法,不是SENet中的逐点相乘, 在这里相当于是对每个像素点的所有通道,进行加权求和, 得到一个总的通道特征
所以说shape是$1×H×W$ , 总体上可以把这一部分理解为 使用 1×1 分支生成的权重,调整3×3尺度的特征, 从而得到当前尺度下的全局空间注意力表示,也就是 $1×H ×W $
🟢 再来看右边分支
在3×3分支的输出基础上,执行一个池化操作和softmax操作,得到归一化之后的通道描述符,也就是 $ 1×\frac{C}{G}$, 然后以这个1×1尺度的输出进行矩阵乘法,得到shape为$ 1×H×W $的输出, 相当于用$3×3$分支生成的权重,来调整1×1尺度的特征, 得到的就是3×3尺度下的全局空间注意力表示,也就是 $ 1×H×W $ ,
这两个空间注意力分别表示了不同尺度的空间位置信息
例如左边这个尺度,保存的特征图是3×3的特征图
第二个尺度保存的特征图是1×1尺度的
最后将这两个空间注意力进行相加,并且再次通过Sigmoid函数来生成权重,并且调整输入
🚩 对我们的启示
当简化模型图时,实际上就是一个输入,分别通过$1×1$卷积和$3×3$卷积,然后,两部分的输出进行跨空间信息聚合,简单来说,作者就是是提出了一种新的交互策略,
所以我们在想idea的时候,就可以按照这种方式来,在对两个表示进行融合的时候,不妨替换或者尝试一下这种交互策略,增加创新,提高效果