TDformer讲解

from : 论文研读之时间序列预测：趋势分解模型TDformer

题目划重点: Rethinking Attention for Time-Series Forecasting

在时间序列预测领域重新思考注意力机制的作用

  • 文章的作者美国在读的PHD, 在亚马逊AI实验室实习期间的文章
  • 文章相对来说也比较短小

总结评论：这篇文章将时间序列分解为了趋势性和季节性两个方面，并分别针对不同的数据使用不同的模型，对于时间序列预测具有较好的参考性；实验详实，实验结果对应了文中给出的结论，具有一定的实际应用价值。

问题引入

  • attention的计算就是 softmax, QK,然后再乘以V
  • 当前做 Attention 的域
  1. 最开始就是在时域里面做,比如 informer, Autoformer 都是做时域中计算 Attention
  2. 接着就有文章,在傅立叶频域和小波变换频域做 Attention
  3. 比如傅里叶频域中有代表性的文章: FEDFormer

研究动机

本文的研究动机: 什么样的时间序列机制适合在哪些域里去使用

贡献

主要贡献就是三个

  1. 通过数学的方式证明,在线性条件下,在时域,傅里叶变换域,小波变换域的注意力模型具有相同的表征能力
  2. 第一个贡献中说的是在线性条件下,也就是在linear条件下,还需要考虑非线性的情况,比如 softmax 的情况,softmax函数是一个非线性函数,考虑加入softmax,此时对于季节性数据,趋势性数据,以及噪声尖峰的数据,对哪一个域下做注意力模型效果好,然后给出了相应的结论,也对应了文中的实验
  3. 第三点基于前两个的数学推论和实验结果,作者提出了 TDformer(Trend Decomposition Transformer),首先被趋势进行分解,根据各个趋势适合用什么样的注意力机制,去做什么样的注意力机制

关于第二个贡献 涉及 softmax 的结论:

  1. 对于具有较强季节性的数据:频域注意力模型表现更好,更具有样本效率
  2. 对于具有趋势的数据,注意力一般表现出较差的泛化能力
  3. 对于含有噪声尖峰的数据:频域注意力模型对这种尖峰数据更加稳健

第一个创新点

数学证明

先给出三个域下的注意力机制

  • 首先最基本的就是时域下的注意力机制,就是QKV,softmax QK,然后乘以V

  • 在傅立叶域里面,把QKV分别做了傅立叶变换,然后把它们做了傅立叶变换之后的结果,在傅立叶的频域下做乘积,之后再把结果做一个反变换得到结果

  • 小波变换是相对更麻烦一些,文中举的例子,说小波变化,需要把每一个Q分别它拆成两个,然后再把QKV的两种分别去做结果,然后再返回结果,回到时域

数学推导是比较简单的(不语-.-),因为是要证明在线性条件下,所以这里不考虑softmax,这里的激活函数,就是一个普通的线性注意力机制

首先看时域和傅里叶域的等价性证明

(需要的知识点)

(1) 线性代数矩阵的变换

(2)把傅立叶变换写成矩阵的形式

(3)性质:①逆=共轭转置②对称

接下来小波变换域

  • 小波分解的矩阵具有正定性
  • …

总之,结论:在给定的线性假设下,时域 傅立叶 小波变换的注意力模型是等价的

那么它们的不同就会体现在非线性的条件下,softmax 的影响

非线性的 softmax 对不同注意力的影响

什么是 softmax

在讲这个softmax影响之前, 先说一下softmax是干嘛的

softmax 又叫 归一化指数函数

softmax 的计算本身是带了很多的指数操作的

将一个 K 维的向量通过softmax映射到另一个K维的向量

效果就是从一个向量元素转化成一个概率分布,概率分布也就意味着各个元素的值都在0和1之间,所有元素的和加起来都是等于1

那么在注意力机制里面, 这种概率分布就可以反映为权重分配,权重越高,在注意力机制里受关注的程度也就越高,这个是softmax本身在注意力机制的体现和应用

实验

第一个实验

固定季节性的数据

首先是对于具有季节性的数据

首先是使用预定义的数据来说明叫结论,先用$sin x$函数,来作为这种具有固定季节性的数据,也就是周期性是固定的

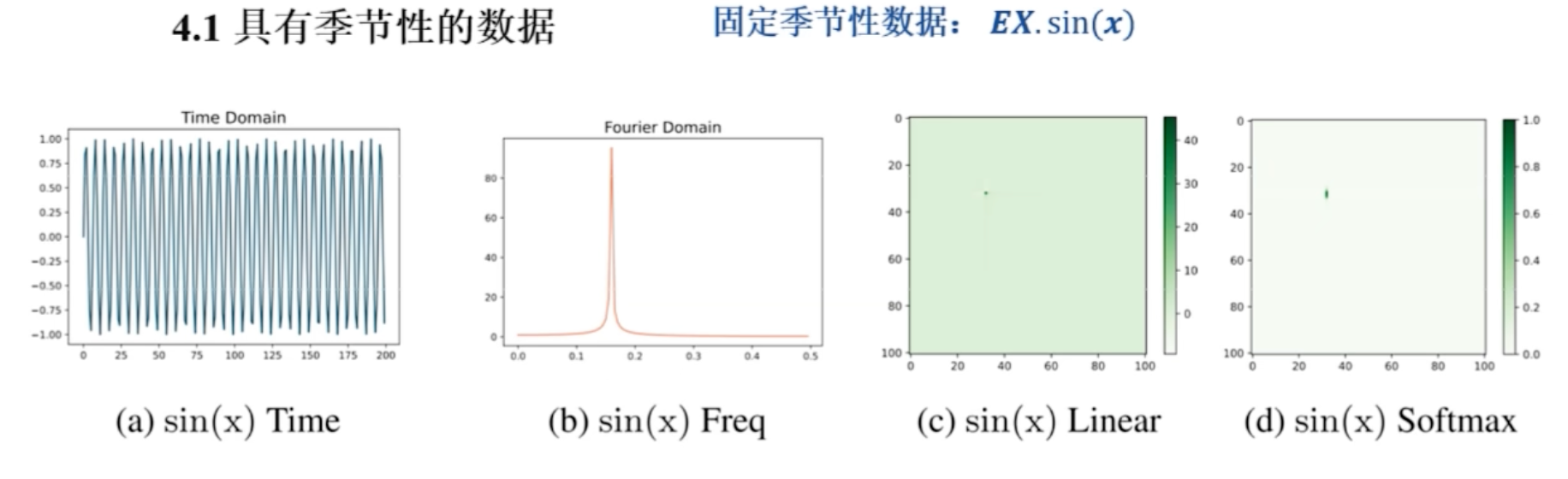
image-20250502153343960

第一个图表示它在时域里的 $\sin x$ 的图形

(b)图,频域下 $\sin x$的图形

(c),(d)后面两个图一个是线性注意力机制时,计算的注意力结果,另一个是加了 softmax 的注意力结果,比较后面两个图可以看到 softmax 具有极化效果应,这是因为 softmax 中的指数运算会加大最大值和最小值之间的差距,大的更大,小的更小

由于极化效应, softmax能够将分数集中在主导频率上,有助于模型更好地捕捉季节性信息

结论:softmax 的极化效应将分数集中在主导频率上,有助于模型更好的捕捉季节信息

以上是固定季节性数据的讲解

三个域下,谁的表现更好

接下来讨论,三个域下,谁的表现更好

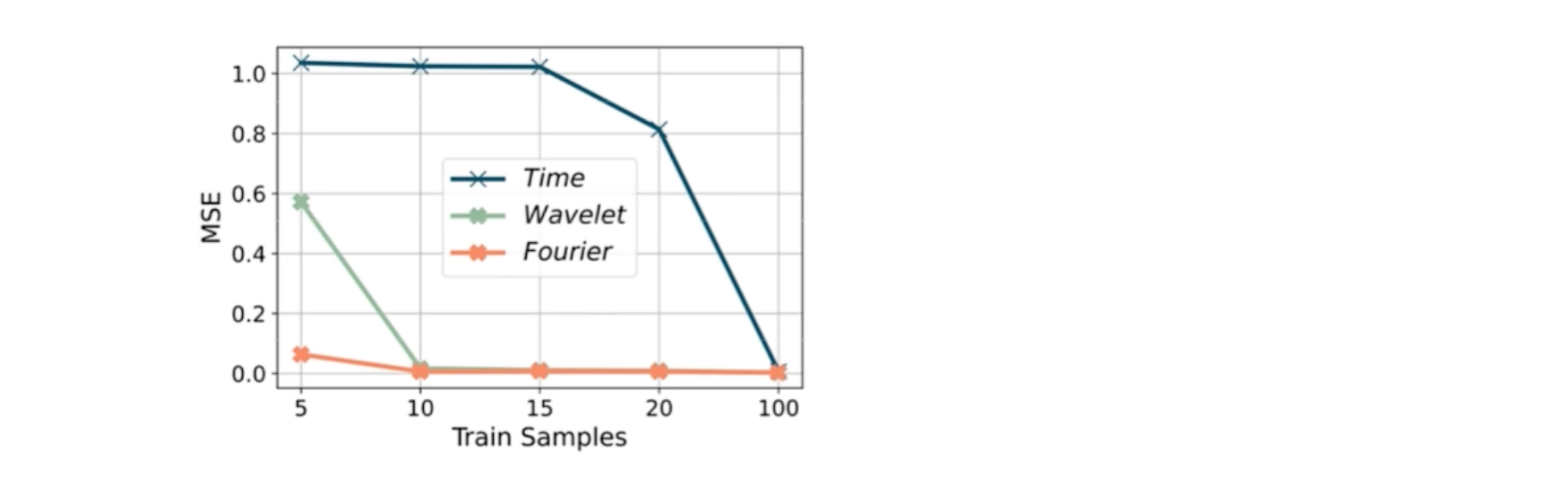
image-20250502154253075

横轴是train samples,样本数量

纵轴是它的那个评估的指标,用多少的样本数量,能够达到零值,就是预测完全

这个图得出来的结论: 在频域注意力模型下,能够快速的识别主频模式

黄线: 傅里叶域,在傅里叶域采样效率是最高的,所以对于季节性数据用傅里叶域+softmax的效果是最好的

结论: 对于季节性数据用傅里叶域+softmax的效果是最好的

这是第一个实验得出来的结论

第二个实验: 变化季节性数据

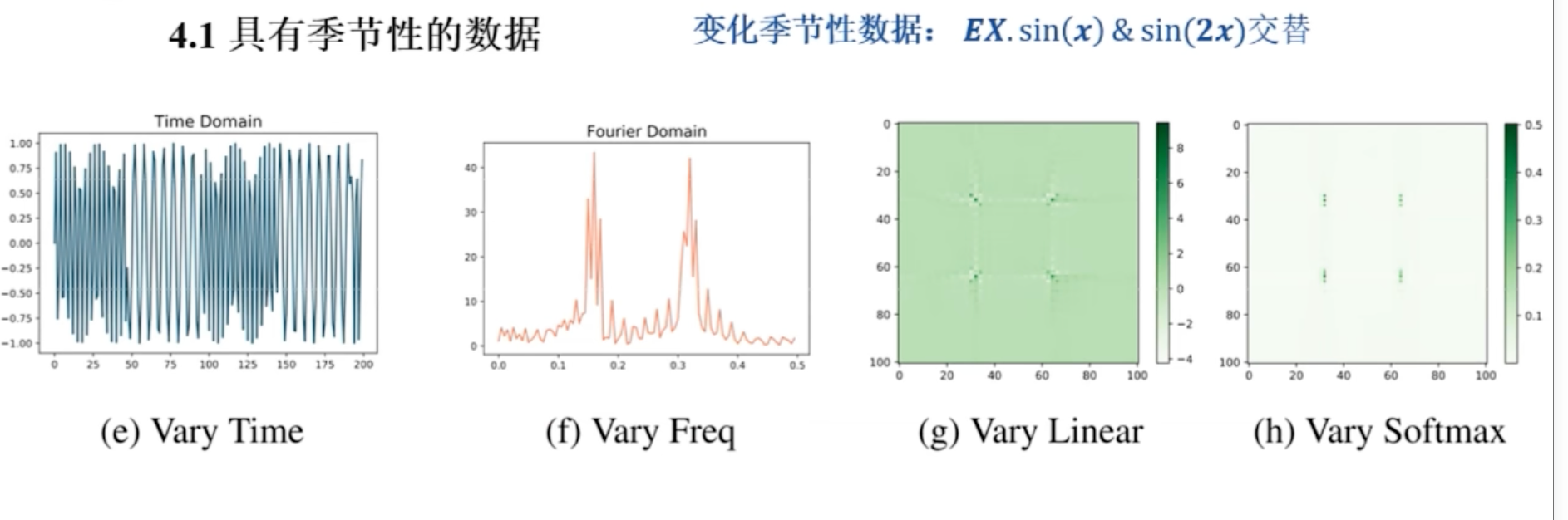
image-20250502154615063

第二个实验也是季节性数据,是 $\sin x$ 和 $\sin2x$ 的拼接

同样,第一个图是 时域,第二个图是 频域, 第三张图 线性注意力机制下的图,第四个,softmax 注意力的图

还有效率的比较

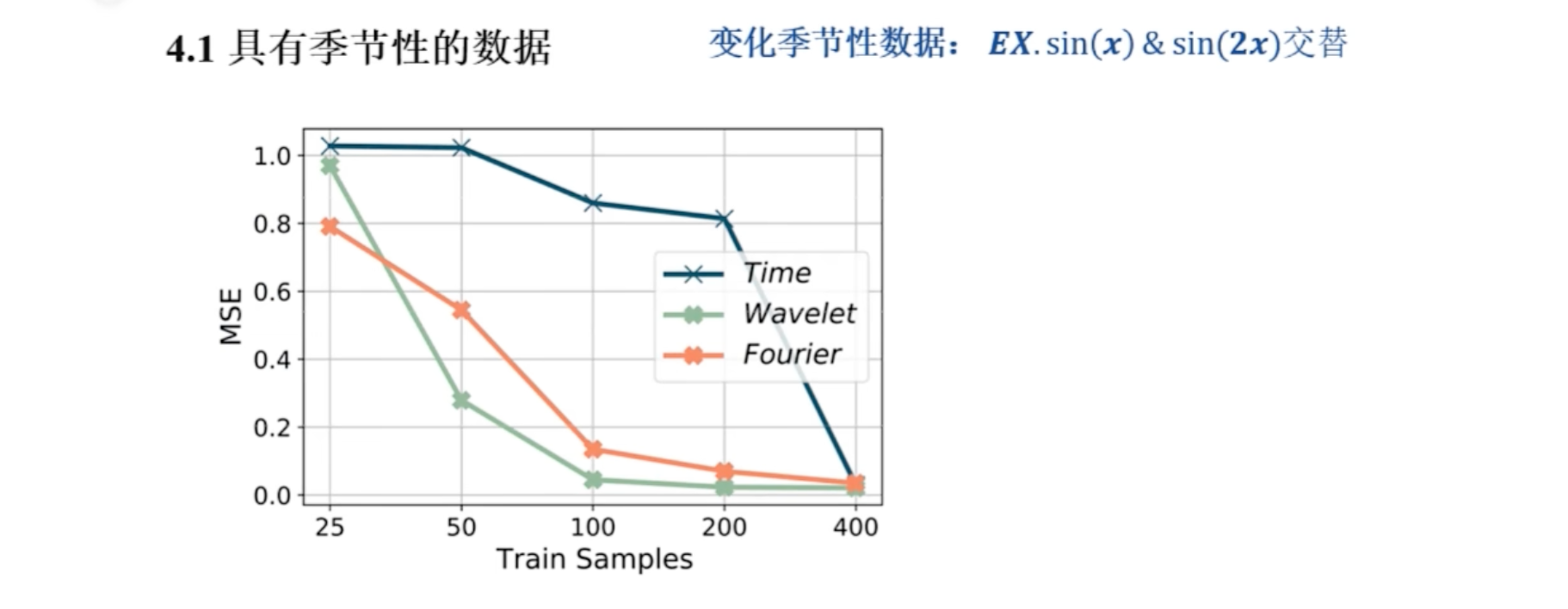
image-20250502175352753

这里的结论: 小波注意结合多尺度时频表示,提供更好的局部频率信息

结论围绕着 ① softmax 有用 ② 频域下效果更好

趋势性数据

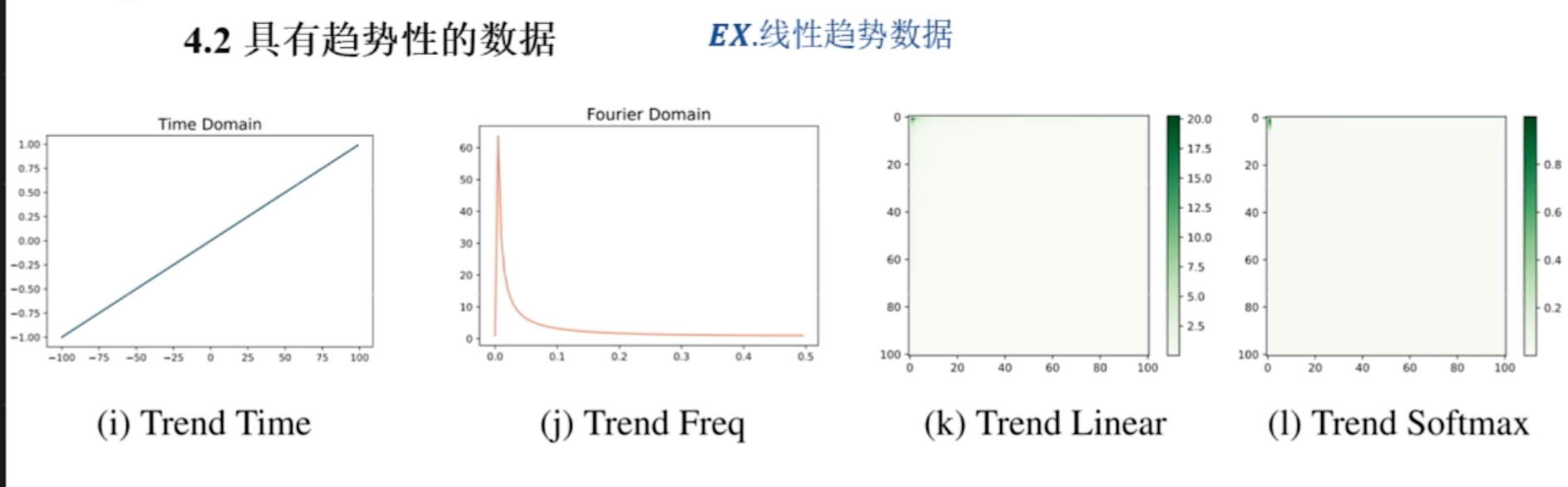
image-20250502175654758

考量了这种具有趋势性的数据

  • 使用线性趋势相关性的数据
  • 后两张图是趋势数据的线性注意力图和 softmax 注意力图,可以看到注意力值集中在左上角
  • 得出的结论: 在 softmax 的极化效应之下,会更强调低频成分,也是强调大值, 但是大值在具有趋势性的数据的时候, 大值反映的是它的低频成分,此时强调低频成分,模型的泛化能力会很差

结论: 在 softmax 的极化效应下,注意力分数更强调低频成分,导致模型在趋势性数据上,泛化能力差

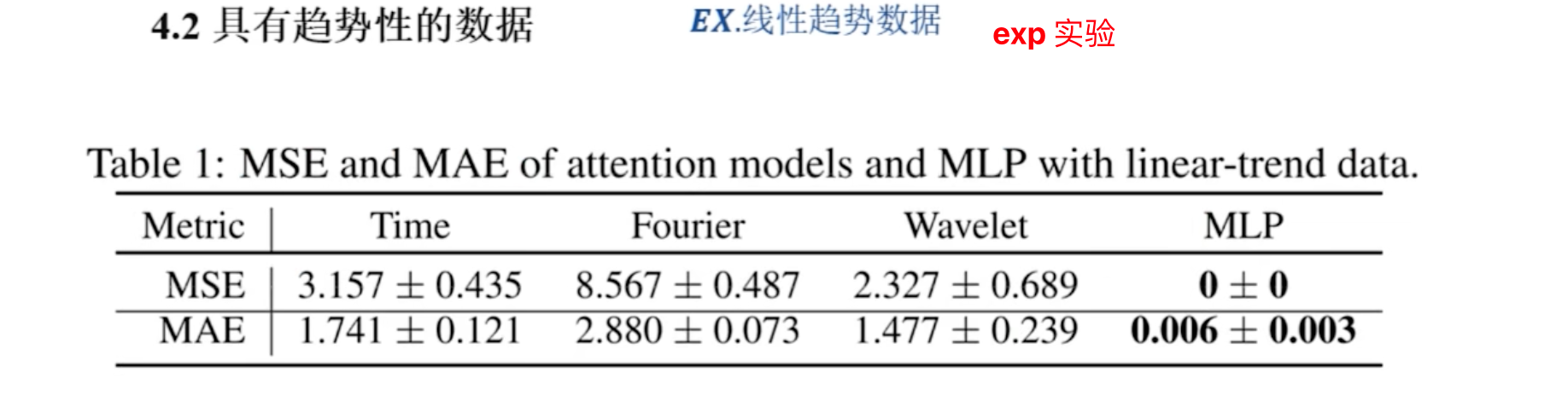
image-20250502180338627

  • 作者又用了定量数据表格,考量趋势性的数据

  • 分别用时域注意力,频域注意力,和 MLP 多层感知机,分别做实验,可以看到多层感知机效果最好

这里得到的结论: 趋势性数据上,注意力机制是不好用的,相反 MLP 能够完美的预测趋势信号

第三个: 带有尖峰的数据

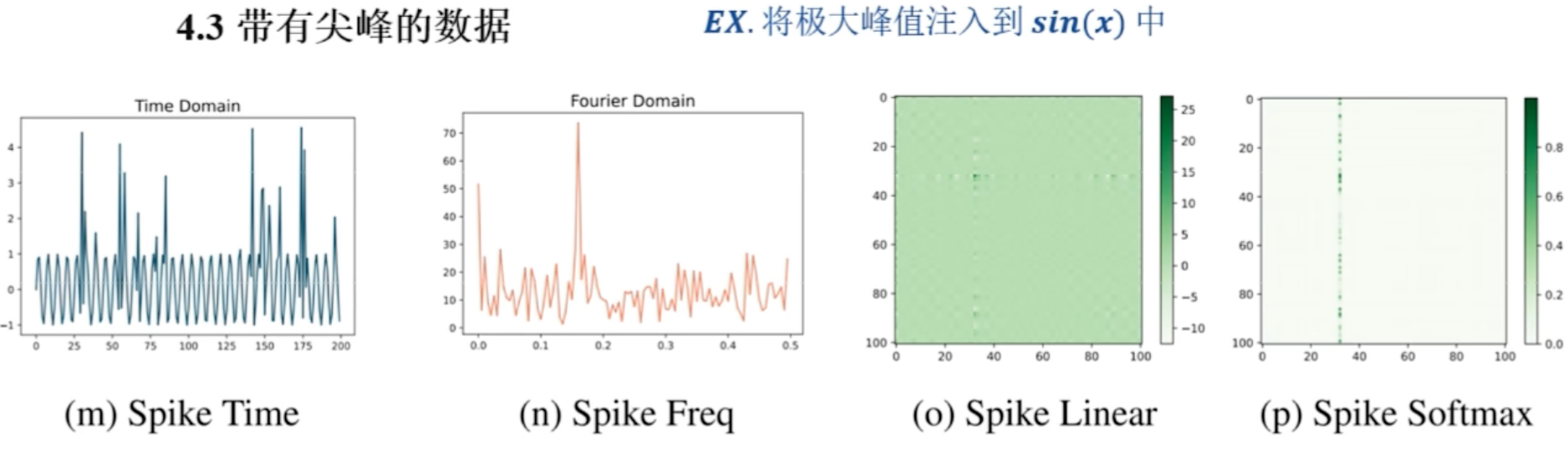
image-20250502180750473

对于带有尖峰的数据集,使用的数据集也是 $\sin x$ , 然后在 $\sin x$ 中,随机的注入峰值

  • 描述图:

第一个图: 时域下可视化

第二个图: 频域下的可视化

后面依然是两个注意力的图

  • 分析图
  1. 在频域下,尖峰会变得弱一些
  2. 在频域中,尖峰变弱了,此时在进行注意力模型,对尖峰的处理,鲁棒性更强,而不会直接聚焦到最大尖峰上

这里的结论:

频域注意力模型,对尖峰的鲁棒性更强

模型

依据文中的分析以及所得到的结论,作者设计了自己的模型

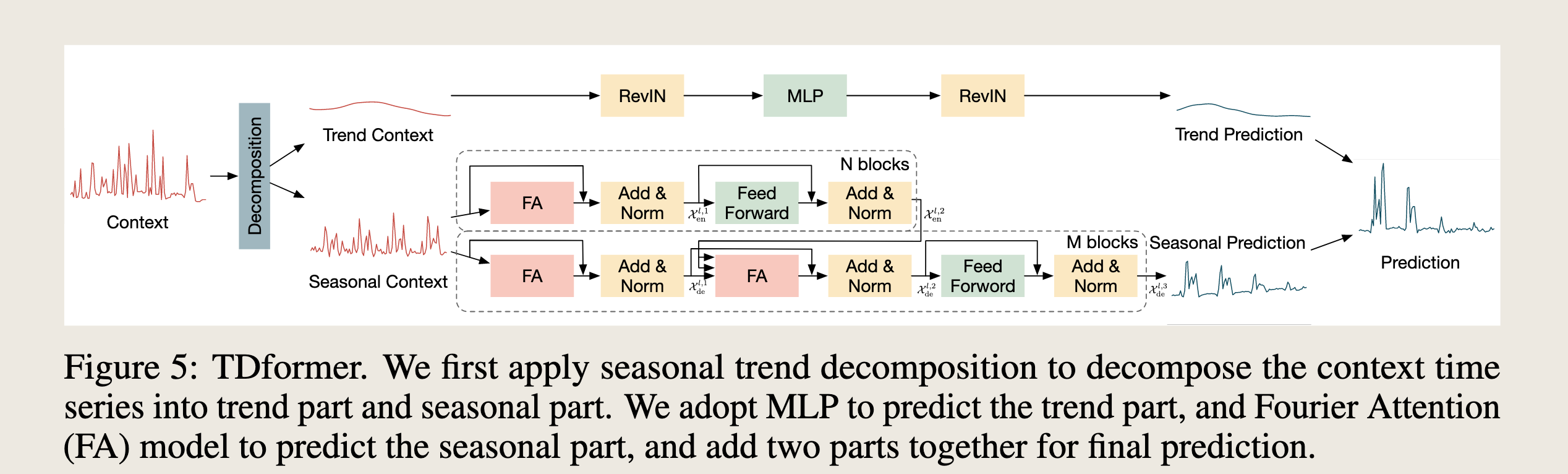
image-20250502181442117

image-20250502181457207

  • 描述模型
  • 模型结构比较简单
  • 首先进行时序分解,将时间序列分成 趋势项和季节项
  • 得到趋势项以后,使用 MLP 预测趋势性
  • 季节项,使用 Transformer 的多头注意力机制,并且使用的是傅里叶频域的注意力机制
  • 最后合并预测结果
👾 本站运行时间:
发表了59篇文章 · 总计11万6千字
© 2025 dearRongerr
使用 Hugo 构建
主题 Stack 由 Jimmy 设计