TimesNet代码复现第一篇

模型结构

TimesNet

Model( (model): ModuleList( (0-1): 2 x TimesBlock( (conv): Sequential( (0): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(16, 32, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(16, 32, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(16, 32, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(16, 32, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) ) (1): GELU(approximate='none') (2): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(32, 16, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(32, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(32, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(32, 16, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(32, 16, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(32, 16, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) ) ) ) ) (enc_embedding): DataEmbedding( (value_embedding): TokenEmbedding( (tokenConv): Conv1d(7, 16, kernel_size=(3,), stride=(1,), padding=(1,), bias=False, padding_mode=circular) ) (position_embedding): PositionalEmbedding() (temporal_embedding): TimeFeatureEmbedding( (embed): Linear(in_features=4, out_features=16, bias=False) ) (dropout): Dropout(p=0.1, inplace=False) ) (layer_norm): LayerNorm((16,), eps=1e-05, elementwise_affine=True) (predict_linear): Linear(in_features=96, out_features=192, bias=True) (projection): Linear(in_features=16, out_features=7, bias=True) )

🔴 单独摘出 TimesNet调试时,会提示

1

run.py: error: the following arguments are required: --task_name, --is_training, --model_id, --model, --data

解决:

删除 require=true

🔴 查看模型参数

❌

1

pip install torchsummary

理由: 只接收一个参数

✅ 使用:

① 安装库 ② 导入库 ③使用

1

pip install torchinfo

实例:

1
2
3
4


from torchinfo import summary

model = Model(args)
summary(model, input_data=[x_enc, x_mark_enc, x_dec, x_mark_dec])

🔵 初始化模型,然后输入 input_data 即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


===============================================================================================
Layer (type:depth-idx)                        Output Shape              Param #
===============================================================================================
Model                                         [32, 24, 7]               --
├─DataEmbedding: 1-1                          [32, 12, 512]             --
│    └─TokenEmbedding: 2-1                    [32, 12, 512]             --
│    │    └─Conv1d: 3-1                       [32, 512, 12]             10,752
│    └─TimeFeatureEmbedding: 2-2              [32, 12, 512]             --
│    │    └─Linear: 3-2                       [32, 12, 512]             2,048
│    └─PositionalEmbedding: 2-3               [1, 12, 512]              --
│    └─Dropout: 2-4                           [32, 12, 512]             --
├─Linear: 1-2                                 [32, 512, 36]             468
├─ModuleList: 1-5                             --                        (recursive)
│    └─TimesBlock: 2-5                        [32, 36, 512]             --
│    │    └─Sequential: 3-3                   [32, 512, 6, 6]           599,800,832
│    │    └─Sequential: 3-4                   [32, 512, 18, 2]          (recursive)
│    │    └─Sequential: 3-5                   [32, 512, 4, 9]           (recursive)
│    │    └─Sequential: 3-6                   [32, 512, 9, 4]           (recursive)
│    │    └─Sequential: 3-7                   [32, 512, 1, 36]          (recursive)
├─LayerNorm: 1-4                              [32, 36, 512]             1,024
├─ModuleList: 1-5                             --                        (recursive)
│    └─TimesBlock: 2-6                        [32, 36, 512]             --
│    │    └─Sequential: 3-8                   [32, 512, 6, 6]           599,800,832
│    │    └─Sequential: 3-9                   [32, 512, 4, 9]           (recursive)
│    │    └─Sequential: 3-10                  [32, 512, 1, 36]          (recursive)
│    │    └─Sequential: 3-11                  [32, 512, 12, 3]          (recursive)
│    │    └─Sequential: 3-12                  [32, 512, 2, 18]          (recursive)
├─LayerNorm: 1-6                              [32, 36, 512]             (recursive)
├─Linear: 1-7                                 [32, 36, 7]               3,591
===============================================================================================
Total params: 1,199,619,547
Trainable params: 1,199,619,547
Non-trainable params: 0
Total mult-adds (T): 6.91
===============================================================================================
Input size (MB): 0.05
Forward/backward pass size (MB): 1432.94
Params size (MB): 4798.48
Estimated Total Size (MB): 6231.47
===============================================================================================

关于这个输出,有两点想说

① 模型参数数量分析,会很多吗?

②数据的流动过程

现就第二点开始说明

数据的流动过程

首先这里的编号怎么理解:

表示模型层级结构 , 如

第一个数字：表示层的深度（depth level）

1 表示顶层模块

2 表示第二层（嵌套在顶层模块内）

3 表示第三层（嵌套在第二层模块内）

依此类推

第二个数字：表示在该深度层级的索引

例如，1-4 表示在第一层深度中的第四个模块

1-4 第 1 层的第 4 个模块

2-3 第 2 层的地三个模块

接下来是 (recursive) ,这个参数别管了, 大概就是控制参数计算的,不懂,不重要
描述数据流动过程

输入数据

x_enc: [32, 12, 7] (批大小, 序列长度, 特征维度)
x_mark_enc: [32, 12, 4] (时间特征)
x_dec: [32, 24, 7] (解码器输入)
x_mark_dec: [32, 24, 4] (解码器时间特征)

DataEmbedding层

将输入数据 [32, 12, 7] 通过三种嵌入转换为 [32, 12, 512]：

TokenEmbedding: 特征嵌入，使用Conv1d (7→512)
TimeFeatureEmbedding: 时间特征嵌入，线性层 (4→512)
PositionalEmbedding: 位置编码 (固定编码)

第一个Linear层

变换数据形状为 [32, 512, 36]，这里36 = 12(输入长度) + 24(预测长度)

TimesBlock层 (第一个)

处理数据保持形状 [32, 36, 512]
内部包含多个Sequential模块，分别处理不同频率模式
Sequential模块: [32, 512, 6, 6]、[32, 512, 18, 2]等表示不同的分解视图

LayerNorm层

对TimesBlock输出进行归一化，形状不变 [32, 36, 512]

TimesBlock层 (第二个)

进一步处理特征，形状仍为 [32, 36, 512]
包含不同的频率分解视图

最后的LayerNorm和Linear

最终Linear层将形状从 [32, 36, 512] 转换回 [32, 36, 7]
最终输出取前24个时间步，得到 [32, 24, 7]

参数分析

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13



关于最后的参数输出:
 ===============================================================================================
Total params: 1,199,619,547  总参数量: 约12亿参数 (1,199,619,547)
Trainable params: 1,199,619,547 可训练参数: 12亿参数 (100%)
Non-trainable params: 0 非训练参数: 0
Total mult-adds (T): 6.91 总乘加运算量: 6.91 T (万亿次操作),前向传播的计算复杂度，影响推理速度
===============================================================================================
Input size (MB): 0.05 单批次输入数据的内存占用  0.05 MB
Forward/backward pass size (MB): 1432.94 前向/后向传播内存: 1432.94 MB (约1.4 GB),训练过程中激活值和梯度的内存占用
Params size (MB): 4798.48 参数内存: 4798.48 MB (约4.8 GB),模型权重的存储空间
Estimated Total Size (MB): 6231.47 总内存估计: 6231.47 MB (约6.2 GB),训练时的总内存占用预估
===============================================================================================

经过以上分析, 这个模型需要至少8GB显存的GPU才能有效训练，考虑到模型本身需要约6.2GB内存, CUDA运行时和其他系统开销需要额外内存, 若需更快训练，可考虑使用更大批量，需要更多显存, 12亿参数的模型规模较大，训练和部署都需要强大硬件支持.

注意这里的例子是使用的是 [32,12,7] → [32,24,7], 因为用 [32,96,7]→[32,720,7] 我的电脑直接内存不足.

所以我让 gpt 帮我分析了一下 [32,96,7]→[32,720,7] 这种情况的参数量

▶️ 主要影响因素：

输入+输出序列总长度从36(12+24)增加到816(96+720)，增加了约22.7倍 TimesBlock中的频率分解处理将处理更长的序列

估计参数量：约 26-30亿参数

▶️ 内存占用预估：

参数存储：约10-12 GB

总训练内存：约15-18 GB

▶️ 计算资源需求

显存需求：至少20GB显存的GPU

训练时间：比原始配置慢3-5倍

推理速度：单次推理可能需要更多计算资源

这段的意思就是想说,这个模型太大了.

进入forcast forward

1

def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):

首先进行标准化

1
2
3
4
5
6


# Normalization from Non-stationary Transformer
means = x_enc.mean(1, keepdim=True).detach()
x_enc = x_enc - means
stdev = torch.sqrt(
    torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
x_enc /= stdev

计算每个特征在时间维度上的均值（维度1）
keepdim=True 保持维度形状 [batch_size, 1, features]
detach() 分离梯度计算，均值不参与反向传播
从原始输入中减去均值，使数据均值为0
计算去均值后数据的标准差
unbiased=False 使用n而非n-1作为除数
1e-5 添加小常数防止除零错误
将数据除以标准差，使各特征标准差为1

形状变化 :

注意以下的演示参数

1
2
3
4


    args.seq_len = 12
    args.pred_len = 24
    args.enc_in = 7
    args.batch_size = 1

means = x_enc.mean(1, keepdim=True).detach()
x_enc B,T,7→mean dim=1 → B,1,7(按列求导) mean 的形状
x_enc = x_enc - means 形状不变 B,T,7
stdev 形状 B,1,7
x_enc /= stdev 形状不变还是 B,T,7

作用:

① 实例归一化 ② 相对模式变化

处理非平稳性：减轻时间序列中趋势和尺度变化的影响
实例归一化：每个批次独立归一化，适应不同样本的分布特性
聚焦相对变化：模型可以专注于学习序列的相对变化模式
提高数值稳定性：避免不同尺度特征导致的训练不稳定

第一步:标准化,后面第二步 ,数据嵌入

1
2
3
4


# embedding
enc_out = self.enc_embedding(x_enc, x_mark_enc)  # [B,T,C]
enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(
    0, 2, 1)  # align temporal dimension

经过 self.enc_embedding 以后, 数据维度从 [B,T,7]→[B,T,512]
enc_out = self.predict_linear 经过 predict_linear 形状 [B,T,512] → [B,T+P,512]

第一步, 标准化

第二步,embedding

第三步, predict_linear 不懂

第四步, for 循环

1

for i in range(self.layer):

这里 self.layer = 2

下一句 enc_out = self.layer_norm(self.model[i](enc_out))

先看这里的 self.model[i] 是这么个东西:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


(0-1): 2 x TimesBlock(
      (conv): Sequential(
        (0): Inception_Block_V1(
          (kernels): ModuleList(
            (0): Conv2d(16, 32, kernel_size=(1, 1), stride=(1, 1))
            (1): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
            (2): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
            (3): Conv2d(16, 32, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
            (4): Conv2d(16, 32, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
            (5): Conv2d(16, 32, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))
          )
        )
        (1): GELU(approximate='none')
        (2): Inception_Block_V1(
          (kernels): ModuleList(
            (0): Conv2d(32, 16, kernel_size=(1, 1), stride=(1, 1))
            (1): Conv2d(32, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
            (2): Conv2d(32, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
            (3): Conv2d(32, 16, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
            (4): Conv2d(32, 16, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
            (5): Conv2d(32, 16, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))

这个 TimesBlock 是个 (conv)的model Sequential,有三层

(0)层是 inception_Block_V1

(1)层是激活函数

(2)层也是 inception_Block_V1

看这里的 (conv): Sequential 小括号和跟着的东西

TimesBlock 类中通过 self.conv 定义了一个命名子模块

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# self.model的定义
self.model = nn.ModuleList([TimesBlock(configs)
                            for _ in range(configs.e_layers)])
# TimesBlock 中 conv定义 
self.conv = nn.Sequential(
    Inception_Block_V1(configs.d_model, configs.d_ff,
                       num_kernels=configs.num_kernels),
    nn.GELU(),
    Inception_Block_V1(configs.d_ff, configs.d_model,
                       num_kernels=configs.num_kernels)
)

也就是说 (conv): Sequential 的解释

模块名(

(子模块名称): 子模块类型(

子模块内容 )

)

🌈 也就是说 (conv) 表示这是 TimesBlock 类中的一个名为 “conv” 的子模块，而非函数调用的括号

上面是 TimesBlock 的 conv 层的定义名字叫 conv, 类型是一个 Sequential

再看,这里 Sequential 的(0)层没有一个专门的名字,就是 (0)层,类型是 Inception_Block_V1 使用一个新的类定义的

同理,(1) 层也没有一个专门的名字,就是(1)层,类型是 GELU(),是pytorch 的官方类型

(2)层也是,没有专门的名字,就是 (2) 层,类型同样是自定义的 Inception_Block_V1

继续自定义的 Inception_Block_V1 的内部定义

我们只从打印出来的 model 看

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


TimesBlock(
  (conv): Sequential(
    (0): Inception_Block_V1(
      (kernels): ModuleList(
        (0): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1))
        (1): Conv2d(512, 2048, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
        (2): Conv2d(512, 2048, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
        (3): Conv2d(512, 2048, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
        (4): Conv2d(512, 2048, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
        (5): Conv2d(512, 2048, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))
      )
    )

补充一下:

torch.info 可以看模型的输入和输出 from torchinfo import summary

1

summary(model, input_data=[x_enc, x_mark_enc, x_dec, x_mark_dec])

print(model) 可以看模型的定义,全部是操作,

查看模型参数和完整的模型结构:

点击展开

Using GPU Args in experiment: Namespace(activation='gelu', anomaly_ratio=0.25, augmentation_ratio=0, batch_size=32, c_out=7, channel_independence=1, checkpoints='./checkpoints/', d_conv=4, d_ff=2048, d_layers=1, d_model=512, data='ETTh1', data_path='ETTh1.csv', dec_in=7, decomp_method='moving_avg', des='test', device=device(type='cuda', index=0), devices='0,1,2,3', discdtw=False, discsdtw=False, distil=True, down_sampling_layers=0, down_sampling_method=None, down_sampling_window=1, dropout=0.1, dtwwarp=False, e_layers=2, embed='timeF', enc_in=7, expand=2, extra_tag='', factor=1, features='M', freq='h', gpu=0, gpu_type='cuda', inverse=False, is_training=1, itr=1, jitter=False, label_len=48, learning_rate=0.0001, loss='MSE', lradj='type1', magwarp=False, mask_rate=0.25, model='TimesNet', model_id='test', moving_avg=25, n_heads=8, num_kernels=6, num_workers=10, p_hidden_dims=[128, 128], p_hidden_layers=2, patch_len=16, patience=3, permutation=False, pred_len=24, randompermutation=False, root_path='./data/ETT/', rotation=False, scaling=False, seasonal_patterns='Monthly', seed=2, seg_len=96, seq_len=12, shapedtwwarp=False, spawner=False, target='OT', task_name='long_term_forecast', timewarp=False, top_k=5, train_epochs=10, use_amp=False, use_dtw=False, use_gpu=True, use_multi_gpu=False, use_norm=1, wdba=False, windowslice=False, windowwarp=False) =============================================================================================== Layer (type:depth-idx) Output Shape Param # =============================================================================================== Model [32, 24, 7] -- ├─DataEmbedding: 1-1 [32, 12, 512] -- │ └─TokenEmbedding: 2-1 [32, 12, 512] -- │ │ └─Conv1d: 3-1 [32, 512, 12] 10,752 │ └─TimeFeatureEmbedding: 2-2 [32, 12, 512] -- │ │ └─Linear: 3-2 [32, 12, 512] 2,048 │ └─PositionalEmbedding: 2-3 [1, 12, 512] -- │ └─Dropout: 2-4 [32, 12, 512] -- ├─Linear: 1-2 [32, 512, 36] 468 ├─ModuleList: 1-5 -- (recursive) │ └─TimesBlock: 2-5 [32, 36, 512] -- │ │ └─Sequential: 3-3 [32, 512, 6, 6] 599,800,832 │ │ └─Sequential: 3-4 [32, 512, 18, 2] (recursive) │ │ └─Sequential: 3-5 [32, 512, 4, 9] (recursive) │ │ └─Sequential: 3-6 [32, 512, 9, 4] (recursive) │ │ └─Sequential: 3-7 [32, 512, 1, 36] (recursive) ├─LayerNorm: 1-4 [32, 36, 512] 1,024 ├─ModuleList: 1-5 -- (recursive) │ └─TimesBlock: 2-6 [32, 36, 512] -- │ │ └─Sequential: 3-8 [32, 512, 6, 6] 599,800,832 │ │ └─Sequential: 3-9 [32, 512, 4, 9] (recursive) │ │ └─Sequential: 3-10 [32, 512, 1, 36] (recursive) │ │ └─Sequential: 3-11 [32, 512, 12, 3] (recursive) │ │ └─Sequential: 3-12 [32, 512, 2, 18] (recursive) ├─LayerNorm: 1-6 [32, 36, 512] (recursive) ├─Linear: 1-7 [32, 36, 7] 3,591 =============================================================================================== Total params: 1,199,619,547 Trainable params: 1,199,619,547 Non-trainable params: 0 Total mult-adds (T): 6.91 =============================================================================================== Input size (MB): 0.05 Forward/backward pass size (MB): 1432.94 Params size (MB): 4798.48 Estimated Total Size (MB): 6231.47 =============================================================================================== Model( (model): ModuleList( (0-1): 2 x TimesBlock( (conv): Sequential( (0): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(512, 2048, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(512, 2048, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(512, 2048, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(512, 2048, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(512, 2048, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) ) (1): GELU(approximate='none') (2): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(2048, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(2048, 512, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(2048, 512, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(2048, 512, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(2048, 512, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) ) ) ) ) (enc_embedding): DataEmbedding( (value_embedding): TokenEmbedding( (tokenConv): Conv1d(7, 512, kernel_size=(3,), stride=(1,), padding=(1,), bias=False, padding_mode=circular) ) (position_embedding): PositionalEmbedding() (temporal_embedding): TimeFeatureEmbedding( (embed): Linear(in_features=4, out_features=512, bias=False) ) (dropout): Dropout(p=0.1, inplace=False) ) (layer_norm): LayerNorm((512,), eps=1e-05, elementwise_affine=True) (predict_linear): Linear(in_features=12, out_features=36, bias=True) (projection): Linear(in_features=512, out_features=7, bias=True) )

嗯,这个 torch.summary运行挺慢的,打印出来看了,就注释掉把

理由 : summary 会对模型进行一次完整的前向传播以获取每一层的输出形状

使用:

1
2
3
4
5


model = Model(args)
summary(model, input_data=[x_enc, x_mark_enc, x_dec, x_mark_dec])
print(model)
outputs = model(x_enc,x_mark_enc,x_dec,x_mark_dec)
print(outputs.shape)

just my code=True 在两处设置,怎么找这里的设置?

小虫子>下拉框>添加配置

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


    "configurations": [

        {
            "name": "[这里更换为任意名称]",
            "type": "debugpy",
            "justMyCode": true,
            "request": "attach",
            "connect": {
                "host": "localhost",
                "port": 5998
            }
        },

        {
            "name": "Python 调试程序: 当前文件",
            "type": "debugpy",
            "request": "launch",
            "program": "${file}",
            "justMyCode": true,
            "console": "integratedTerminal"
        }
    ]

timeBlock forward

算了,什么都不说了.直接看 TimeBlock forward 把

emm init 是这样的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class TimesBlock(nn.Module):
    def __init__(self, configs):
        super(TimesBlock, self).__init__()
        self.seq_len = configs.seq_len
        self.pred_len = configs.pred_len
        self.k = configs.top_k
        # parameter-efficient design
        self.conv = nn.Sequential(
            Inception_Block_V1(configs.d_model, configs.d_ff,
                               num_kernels=configs.num_kernels),
            nn.GELU(),
            Inception_Block_V1(configs.d_ff, configs.d_model,
                               num_kernels=configs.num_kernels)
        )

主体就是 self.conv = nn.Sequential 用 sequential定义的 (conv) 变量名

可是来看到 forward

1
2
3


   def forward(self, x):
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)

算了先看形状变化把

1

period_list, period_weight = FFT_for_Period(x, self.k)

这里奇怪的点在于不管是直接打印 print(model) 还是 torchinfo summary 都没有出现这一部分 FFT_for_Period

随手补充

主要原因,① **函数而非模块**：FFT_for_Period 是一个普通的 Python 函数，不是 nn.Module 的子类 ②**非模型参数**, 它在 forward 方法中被调用，但不是通过 self. 引用的组件③ **无可训练参数**：该函数没有需要训练的参数，只是一个变换操作 PyTorch 模型摘要工作原理, print(model) 和 torchinfo.summary() 只会显示继承自 nn.Module 的组件, 作为模型属性（通过 self.xxx 方式）注册的层,包含可训练参数的组件

输入 : x.shape = [32,36,512] self.k=5

随手补充

self.predict_linear的定义是Linear(in_features=12, out_features=36, bias=True) 所以从 [32,12,512] 变成 [32,36,512]

输出 : period_list, period_weight 形状

步进,就是这样的定义:

FFT_for_Period

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]

1️⃣ 第一句 xf = torch.fft.rfft(x, dim=1)

x.shape=[32,36,512] → torch.fft.rfft → xf.shape=[32,19,512]

抽象化 [B,T+P,C] → [B,(T+P)//2+1,C]

第二句 frequency_list = abs(xf).mean(0).mean(-1)

(实例讲解) xf.shape=[32,19,512] ->abs(xf)->[32,19,512] -> mean(0) ->[19,512] 沿着拿个维度求 mean,哪个维度变成 1,这里没有保留维度,所以直接变成了 2 维. -> mean(-1) -> [19]

(抽象化讲解)

输入

xf = torch.fft.rfft(x, dim=1)的结果：

形状：[B, T//2+1, C]，其中B是批量大小，T是时间长度，C是特征数

类型：复数张量，包含振幅和相位信息

含义：时间序列x在频率域的表示

处理过程

步骤1：计算频率幅度: abs(xf)

操作：计算每个复数元素的绝对值（幅度）

结果形状：依然是[B, T//2+1, C]

含义：每个频率分量的能量大小，丢弃了相位信息

数学表示：|FFT(x)|

步骤2：批次维度上的平均 abs(xf).mean(0)

操作：在维度0（批次维度）上取平均值

结果形状：[T//2+1, C]

含义：所有批次样本在每个频率、每个特征上的平均能量

效果：减少个体样本波动，获取整体频率特性

步骤3：特征维度上的平均 abs(xf).mean(0).mean(-1)

操作：在维度-1（特征维度）上取平均值

结果形状：[T//2+1]

含义：所有批次、所有特征在每个频率上的平均能量

效果：得到不依赖于具体特征的频率重要性评分

输出

frequency_list是一个一维张量：

形状：[T//2+1]

内容：每个频率点的重要性评分（平均能量）

索引：从低频到高频排序，索引0对应直流分量（0频率）

用途：用于后续选择能量最大的k个频率点

关于torch.fft.rfft(x, dim=1)的补充阅读笔记

①

随手补充: 复数张量，包含振幅和相位信息

xf复数分解后的单个元素是复数,是说这里的 19 ,具体来说就是每个数=a+bi 那就会问了,哪个是振幅,哪个是相位信息嗯,振幅=\sqrt{a^2+b^2} 相位=arctan(b/a)

②

随手补充关于 DFT 离散傅里叶变换的浅薄理解

如果我们有 720 个小时的数据,根据一个定理,我们最多识别的周期是...(最高可识别频率：根据奈奎斯特定理，对于N=720个采样点，最高可识别频率为f_{max} = N/2 = 360,最短可识别周期：T_{min} = 720/360 = 2小时) DFT 就是说计算这 720 小时是一个 2\pi 的可能性,也就是 T=720;转 2 个 2\pi 的可能性,也就是 T=360的可能性,这里的可能性用振幅表示更专业的术语描述: 傅里叶变换是频率描述的语言,可是我们最直观的理解是周期性语言,所以刚开始接触是很别扭的 1️⃣ 对于长度为720小时的时间序列数据,基本频率：f₁ = 1/720 (每720小时完成一个完整周期),对应周期：T = 720小时 2️⃣ 谐波频率： f₂ = 2/720 = 1/360 (每360小时完成一个周期) → T = 360小时 f₃ = 3/720 = 1/240 (每240小时完成一个周期) → T = 240小时 f₄ = 4/720 = 1/180 (每180小时完成一个周期) → T = 180小时 ...以此类推 3️⃣ 最高可识别频率：根据奈奎斯特定理，对于N=720个采样点，最高可识别频率为f_{max} = N/2 = 360; 最短可识别周期：T_{min} = 720/360 = 2小时 ===================================

③

随手补充:关于奈奎斯特定理

意思就是如果有 720 个小时的数据,那么÷2=360 ,也就是最多能识别到的周期是 360 个,每个周期=2 小时 ===================================

④随手补充如果你也很奇怪 DFT 展开式与三角函数形式,复指数形式和复数 a+bi的展开式

三角函数展开形式 $x(t) = a₀ + ∑[aₖcos(2πkt/N) + bₖsin(2πkt/N)]$ , 优点：物理意义明确，直接反映了信号中各频率的振荡成分
复指数展开形式,利用欧拉公式$e^{jθ} = cos(θ) + j·sin(θ)$，可以将三角函数形式改写为更紧凑的复指数形式：$x(t) = ∑Xₖe^{j2πkt/N}$ , 其中$Xₖ$是复数系数。优点：数学表达更简洁，便于理论分析和推导
直接复数表示: 是计算机实现中最常用的形式, $Xₖ = ∑x(n)e^{-j2πkn/N}$, 每个$Xₖ$可以表示为：$Xₖ = |Xₖ|e^{jφₖ}= |Xₖ|(cos(φₖ) + j·sin(φₖ))$ , $|Xₖ|$是幅度（振幅），表示该频率分量的能量, $φₖ$是相位角，表示该频率分量的时间偏移, 优点：直接对应FFT算法的输出，用于编程实现

⑤更准确的理解:

DFT 就是说计算这 720 小时是一个 2\pi 的可能性,也就是 T=720;转 2 个 2\pi 的可能性,也就是 T=360的可能性,这里的可能性用振幅表示

DFT与周期识别的关系, 在处理720小时的时间序列数据时，DFT（离散傅里叶变换）确实是在测量不同周期模式在数据中的存在强度：

基本频率：f₁ = 1/720（每720小时完成一个周期）

这对应于整个序列长度的周期T=720

二次谐波：f₂ = 2/720 = 1/360（每360小时完成一个周期）

对应周期T=360

更高谐波：f₃, f₄, …对应更短的周期T=240, T=180, …

“可能性"这个词不太精确，更准确的说法是：

振幅（幅度）表示该周期模式在原始数据中的贡献强度或能量

振幅越大，表明该周期模式在数据中越显著

好了,我再说一遍,好像更懂了

就是,有 720 个小时的数据,傅里叶假设这串数据是分别由 T=720,T=360,T=180,T=….,T=720/360 (奈奎斯特定理) 的三角函数构成,三角函数的基本构成,振幅,相位,频率 $Asin(2\pi f \times t + \phi)$ 你这样写不好看,人家都是 $sin + cos$ 的形式 ,总之,意思是这样的,现在 $f$ (T 有,f 就有) 有了, 这是一些正交基,然后你就一个个衡量每个周期(频率)的贡献度,也就是 A,

对于长度为N=720的离散时间序列，傅里叶级数的标准表示是：

$$x(t) = a_0 + \sum_{k=1}^{N/2} [a_k \cos(2\pi k t / N) + b_k \sin(2\pi k t / N)]$$

其中：

$a_0$ 是直流分量（平均值）
$a_k$ 是第k个频率的余弦分量系数
$b_k$ 是第k个频率的正弦分量系数
$k$ 对应频率索引，关联到周期 $T = N/k$

周期与频率的对应关系

对于720小时的数据，主要周期及其对应的频率索引：(这是编程出的图的横坐标)

频率索引(k)	周期(T=720/k)	物理含义
1	720小时	整个序列为一个完整周期
2	360小时	两个完整周期（如每15天一个循环）
3	240小时	三个完整周期（如每10天一个循环）
4	180小时	四个完整周期（如每周期循环，一周≈168小时）
24	30小时	24个完整周期（接近每天循环，一天=24小时）
…	…	…
360	2小时	奈奎斯特频率限制（最高可识别频率）

傅里叶系数的计算

对于任意频率索引k：(这里的 $\frac{2}{N}$ 是归一化系数)

$a_k = \frac{2}{N}\sum_{t=0}^{N-1}x(t)\cos(2\pi kt/N)$

$b_k = \frac{2}{N}\sum_{t=0}^{N-1}x(t)\sin(2\pi kt/N)$

系数告诉我们每个频率分量的强度

$$X_k = \sum_{t=0}^{N-1}x(t)e^{-j2\pi kt/N}$$

$X_k = \frac{N}{2}(a_k - jb_k)$ 当 $k \neq 0, k \neq N/2$

$|X_k| = \frac{N}{2}\sqrt{a_k^2 + b_k^2}$ 是幅度

还是举个例子,说明 720 小时的数据中,T=360周期($f=\frac{1}{360}$)存在的强度:

$a₂ = (2/720)·∑x(t)·cos(2πt/360)，从t=0到t=719$

$b₂ = (2/720)·∑x(t)·sin(2πt/360)，从t=0到t=719$

嗯,就是这样的.

对于周期T=360的分量，对应频率索引k=N/T=720/360=2，因此该周期的贡献是：

$a₂cos(2π·2·t/720) + b₂sin(2π·2·t/720) = a₂cos(2πt/360) + b₂sin(2πt/360)$

再看一遍傅里叶展开的三角函数形式 (k从 $0$ 变到 $360$ ( 奈奎斯特定理 ))

$x(t) = a₀ + ∑[aₖcos(2πkt/N) + bₖsin(2πkt/N)]$

$a_0+[a_1\cos(2\pi f_1 t) + a_1 \sin(2 \pi f_1 t)] + {a_2\cos(2\pi f_2 t) + a_2 \sin(2 \pi f_2 t)}+...+$

$f_1 = \frac{1}{720}$

$f_2 = \frac{1}{360}$

最后一个是 $\frac{1}{2}$

也就是所有傅里叶展开最后一个频率都是 $\frac{1}{2}$

傅里叶展开中的频率上限解析

在离散傅里叶变换(DFT)中，对于任何长度的数据序列，最高频率确实始终是 $\frac{1}{2}$。这是数字信号处理中的一个基本原则。

为什么最高频率总是 $\frac{1}{2}$？

这与奈奎斯特采样定理直接相关：

对于采样周期为1的离散信号：

最高可识别频率为每个样本0.5个周期

用归一化频率表示就是 $f_{max} = \frac{1}{2}$

对于长度为N的信号：

可以识别的频率分量有 $\lfloor \frac{N}{2} \rfloor + 1$ 个

频率索引k从0到$\lfloor \frac{N}{2} \rfloor$

对应的归一化频率为 $f_k = \frac{k}{N}$

最高频率为 $f_{max} = \frac{\lfloor N/2 \rfloor}{N} \approx \frac{1}{2}$

在N=720的具体例子中

频率索引(k)	归一化频率(f=k/N)	物理含义
0	0	直流分量(平均值)
1	1/720	基频(整个序列一个周期)
2	2/720 = 1/360	第二谐波
…	…	…
360	360/720 = 1/2	最高频率(奈奎斯特频率)

这就是为什么傅里叶展开的最后一个频率总是 $\frac{1}{2}$ - 它代表每两个样本点完成一个完整周期的分量，这是离散采样信号能表示的最高频率。

嗯,再读一遍这句话: 每两个样本点完成一个周期

继续看这个函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]

xf = torch.fft.rfft(x, dim=1) 这句的解释已经很透彻了

第一句,输入 BTC,在时间步维度上进行 DFT,输出 [B,T//2+1,C]

不过这里更准确的话,应该是 T+P

现在第二句,frequency_list = abs(xf).mean(0).mean(-1), 求均值,先 B 维度上求,然后 C 特征维度上求,最后只留下时间步维度

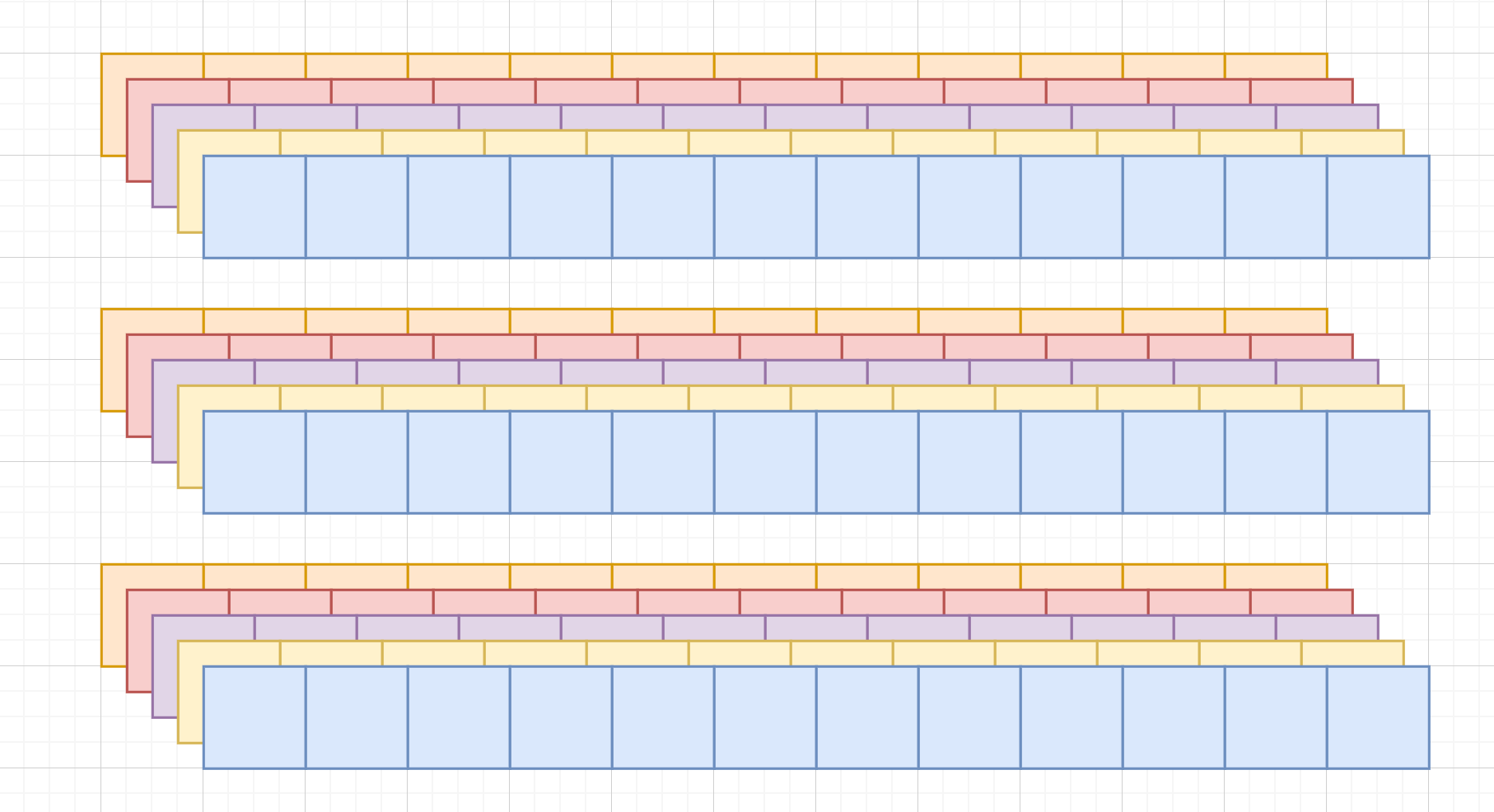
现在 B 维度上求,想象

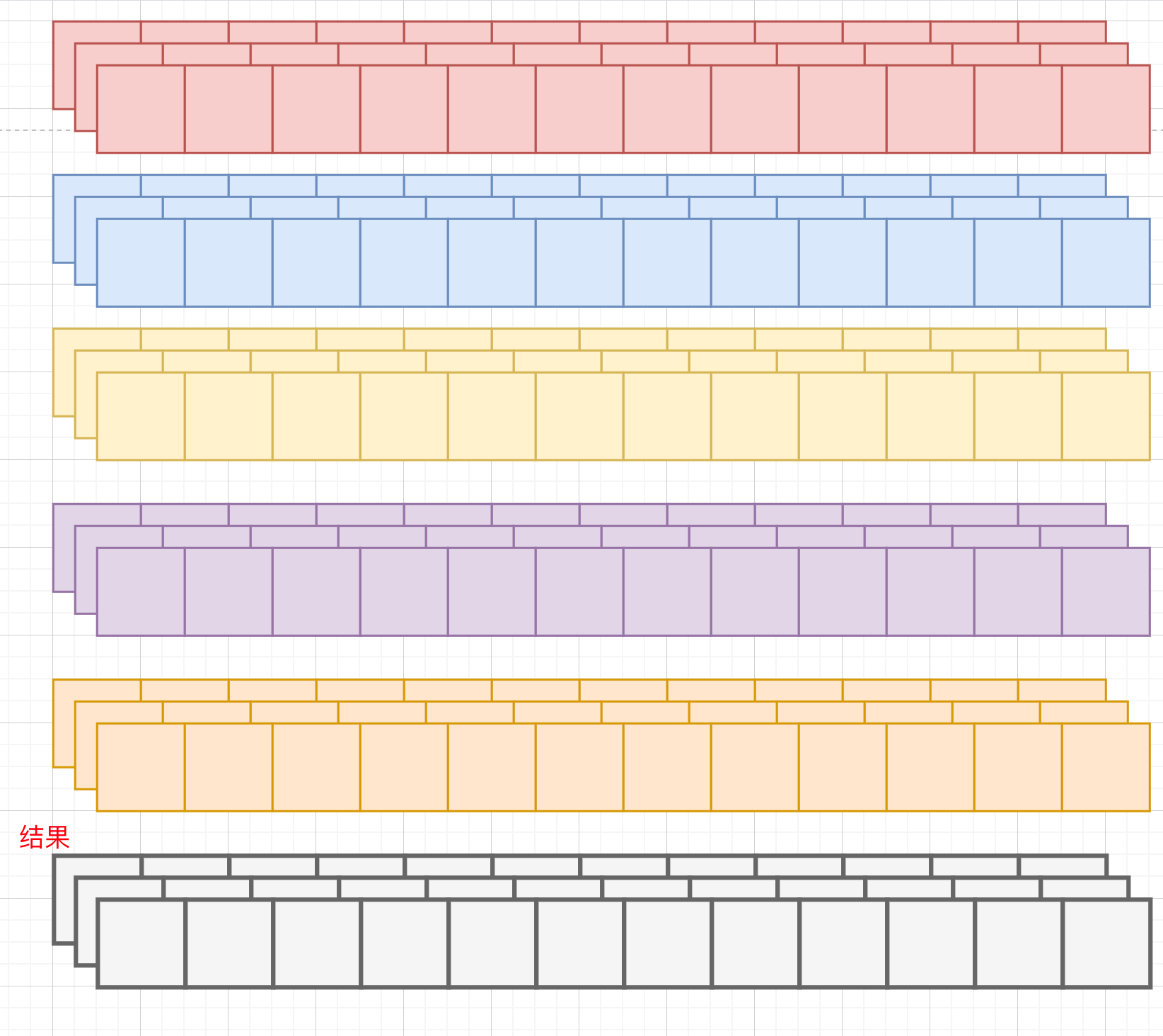
接下来特征维度:

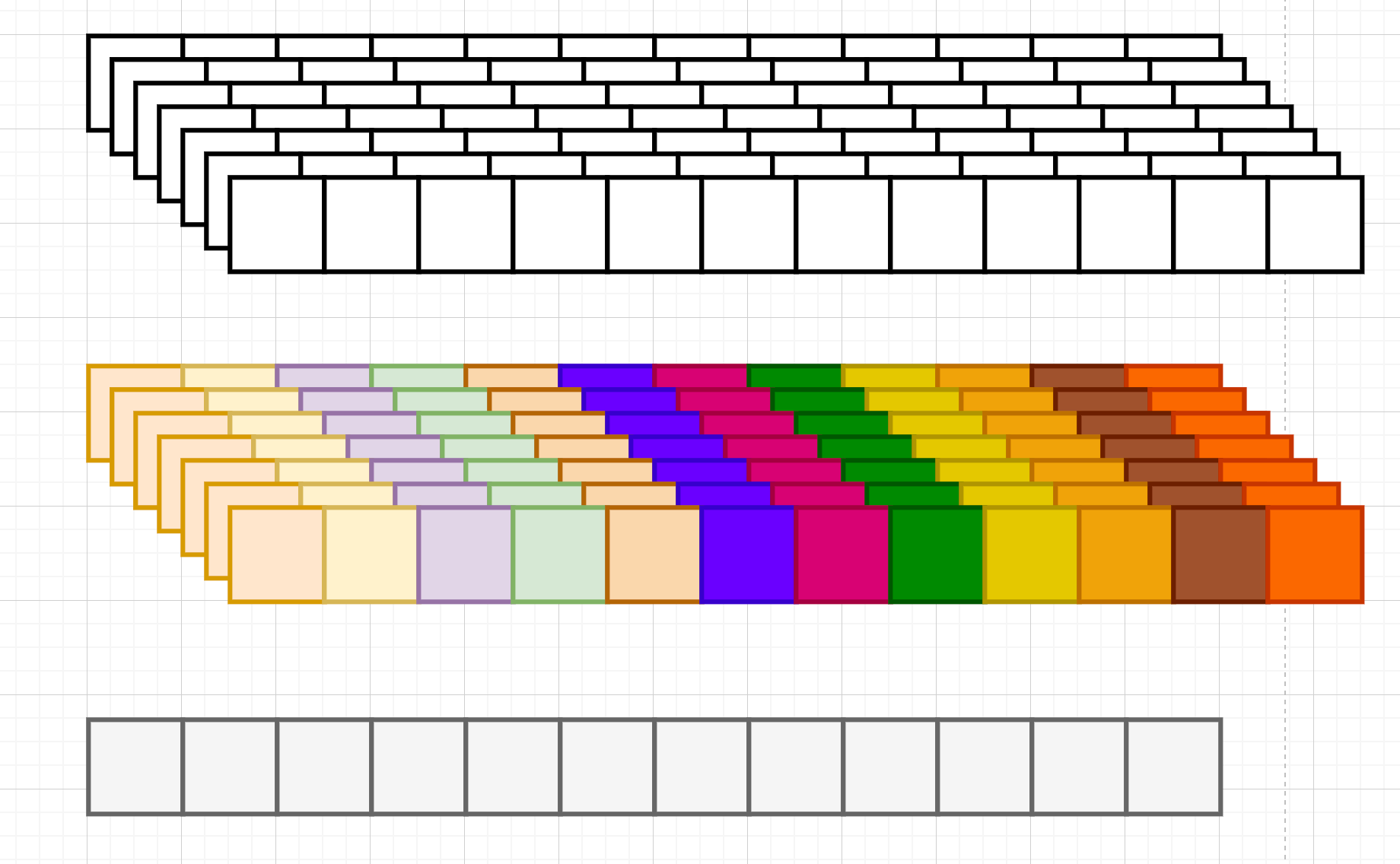
再画一张,每一个小方格都表示一个数字,一个 B 就是一个样本.一个样本由 96 个时间不步组成,每个时间步有 C 个特征,每 32 个样本封装成一个批次,也就是同时处理 32 个样本

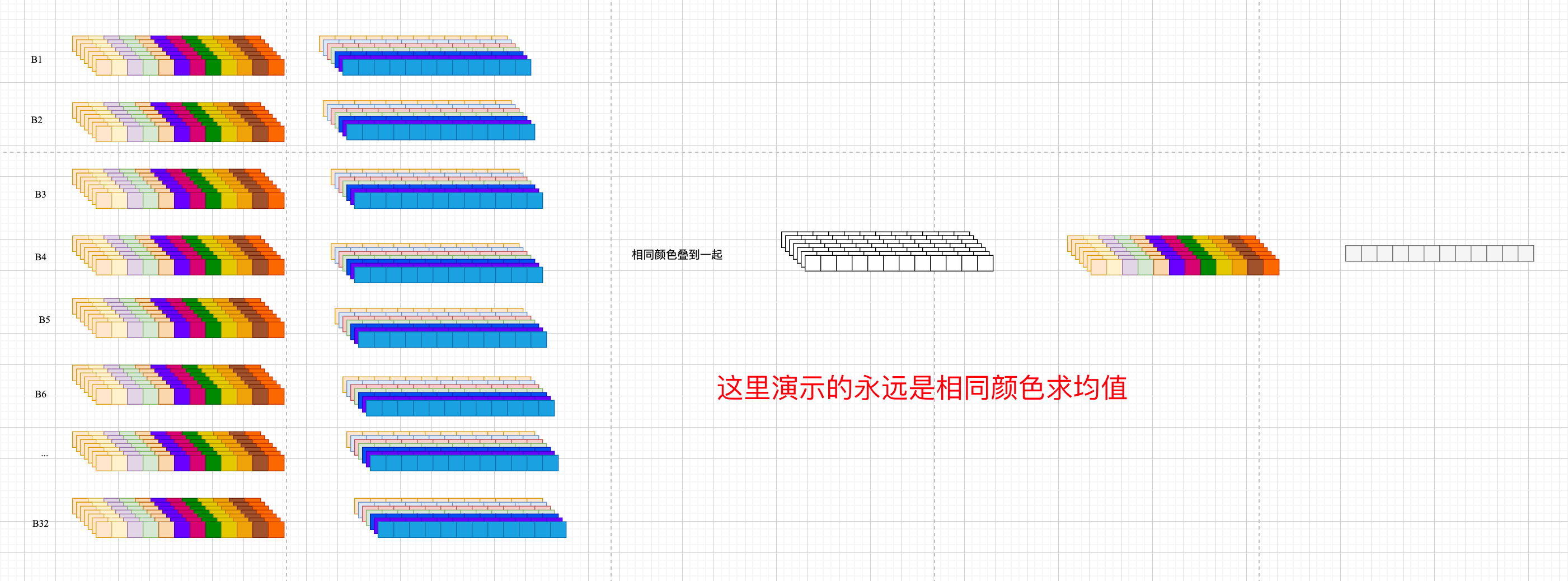
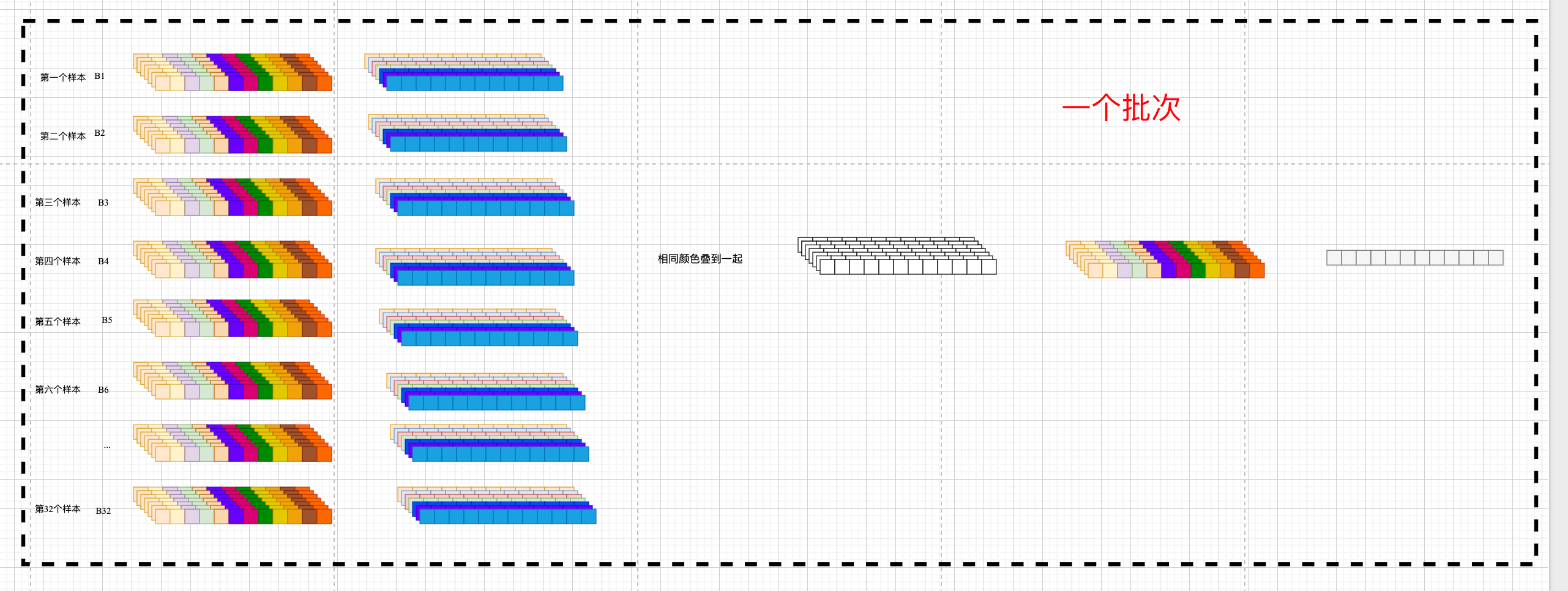
第三句, frequency_list[0] = 0 ,频率值第 0 维赋值=0,

继续看第三句,将零频率分量(直流分量)设为0,频率索引0对应的是直流分量(DC)，代表时间序列的平均值，不包含任何周期信息,直流分量通常具有最大能量，如果不将其排除，后续的torch.topk会将其识别为最重要的"周期”，但它实际上不代表任何周期性, 直流分量置零使模型专注于数据的变化模式，而非静态平均水平,在周期分析中，忽略直流分量是标准做法

一句话: 只关注真正的周期性变化

第四句: _, top_list = torch.topk(frequency_list, k)

首先,frequency_list,长这样,36 个时间步,识别最多 18 个周期,+1 个直流分量,表示振幅值,也就是每个周期或者频率的贡献度

1
2
3


{Tensor: (19,)} tensor([4.2615, 5.8774, 5.3957, 4.2204, 6.0727, 5.1106, 6.4174, 4.1755, 4.8382,
        5.9319, 5.4854, 4.8242, 4.6387, 5.1032, 5.4027, 5.5041, 5.5786, 6.1143,
        3.7927], grad_fn=<MeanBackward1>)

还是从输入和输出的角度叙述,赋值 0

1
2
3
4


frequency_list
{Tensor: (19,)} tensor([0.0000, 5.8774, 5.3957, 4.2204, 6.0727, 5.1106, 6.4174, 4.1755, 4.8382,
        5.9319, 5.4854, 4.8242, 4.6387, 5.1032, 5.4027, 5.5041, 5.5786, 6.1143,
        3.7927], grad_fn=<CopySlices>)

总的来说: 从傅里叶变换得到的频率能量分布中选择最重要的k个频率。

输入:

第一个参数 frequency_list：包含所有频率能量值的一维张量（已经在前一步将直流分量设为0）
第二个参数 k：要选择的顶部频率数量，在TimesNet中这是由 configs.top_k 指定的

返回值

torch.topk() 函数返回两个值：

第一个返回值：选中的k个最大能量值
第二个返回值：这k个最大值在原张量中的索引位置

1

_, top_list = torch.topk(frequency_list, k)

_ 符号：表示我们忽略第一个返回值（能量大小），因为我们只需要知道哪些频率重要，不需要它们的具体能量值

top_list：获取的是k个能量最大的频率的索引

随手补充

进行自动周期识别：能量越大的频率分量，对原始信号的贡献越大选择top-k个频率，就是找出时间序列中最显著的k个周期模式这些频率索引将在后续步骤中转换为实际的周期长度 ===================================

假设我们有频率能量列表：

[0, 0.8, 1.5, 0.3, 0.9, 0.1, …]

对于k=3，torch.topk()会返回：

能量值：[1.5, 0.9, 0.8]

索引：[2, 4, 1]

这意味着索引2、4和1对应的频率（分别对应周期T=N/2, N/4和N/1）是最重要的三个周期模式。

关于这个频率能量表,[直流分量,T=length,T=length//2,T=length//4]

[周期=无穷(直流分量),进行一个周期(时间步长),进行两个周期(二分之时间步长),进行三个周期(三分之时间步长),…..] 这里的理解对于理解后面几句很重要

接下来后面几句

1
2


top_list = top_list.detach().cpu().numpy()
period = x.shape[1] // top_list

找出能量最大的几个频率
计算这些频率对应的周期长度 = 总长度/频率索引

频率与周期的对应关系正是：

频率索引	物理含义	对应周期
0	直流分量	无周期（或无限长周期）
1	完成1个完整周期	T = length
2	完成2个完整周期	T = length/2
3	完成3个完整周期	T = length/3
…	…	…
length/2	完成length/2个周期	T = 2 (最小可识别周期)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]

最后还剩返回值的理解

period 不用说了,就是返回5 个最明显的周期

abs(xf).mean(-1)[:, top_list],这里

xf shape=[B,(T+P)//2+1,C]
mean(-1) [B,(T+P)//2+1]
[:, top_list] [B,5]

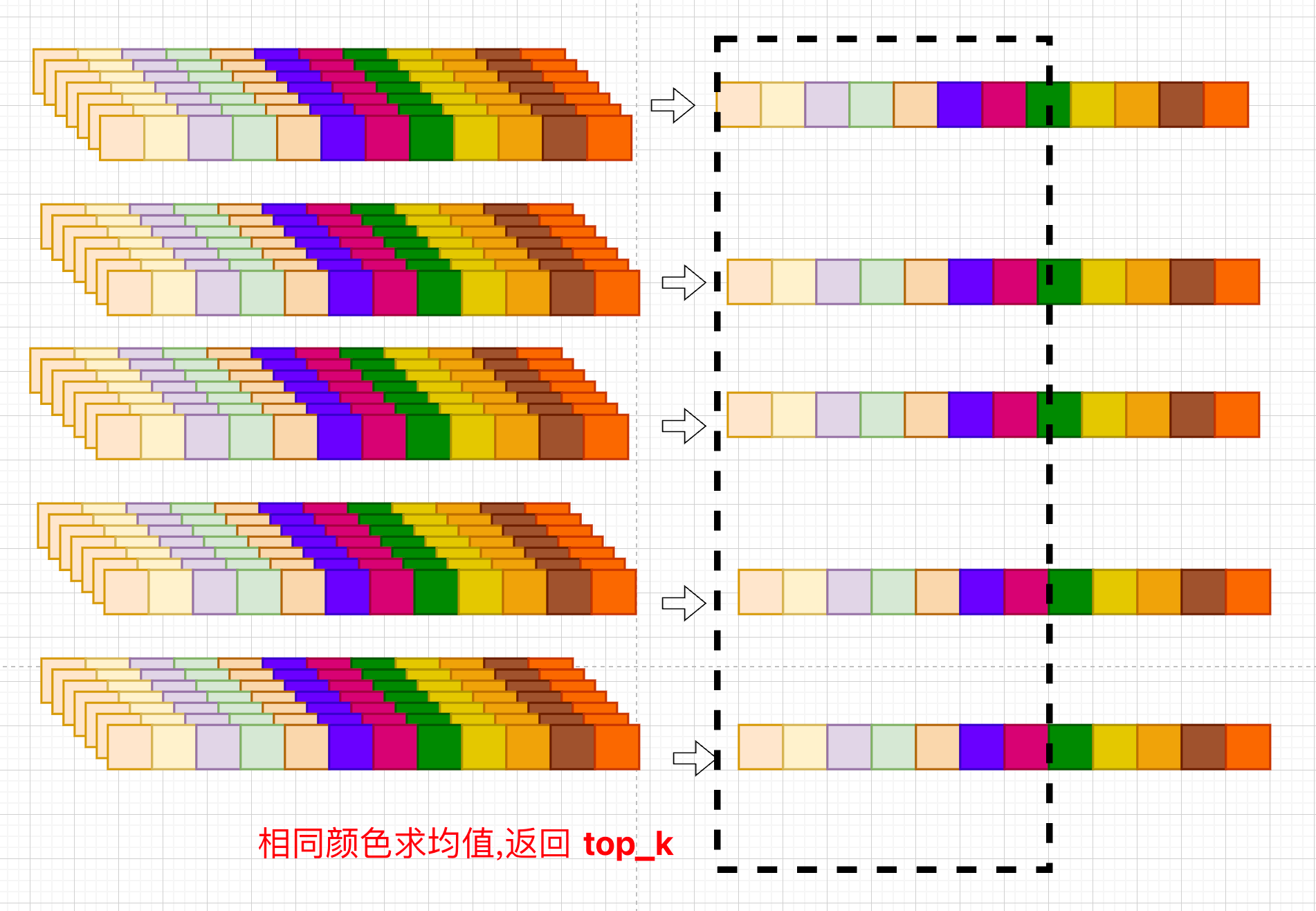
再来看专业点的说法:

第一个返回值：period

类型：numpy数组
形状：[k]（k个元素的一维数组）
内容：识别出的k个主要周期长度
计算方式：x.shape[1] // top_list
示例：对于长度为96的序列，如果top_list=[2,4]，则period=[48,24]，表示周期为48和24的两种模式

第二个返回值：abs(xf).mean(-1)[:, top_list]

类型：PyTorch张量
形状：[B, k]（B是批量大小，k是周期数量）
内容：每个样本在k个主要频率上的能量值

计算过程：

abs(xf)：计算FFT结果幅度，形状[B, T//2+1, C]
abs(xf).mean(-1)：在特征维度上取平均，形状变为[B, T//2+1]
[:, top_list]：只保留k个主要频率的能量值，形状变为[B, k]
用途：作为不同周期模式的权重，用于后续自适应融合

好了,终于执行完了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1) 
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]

[B,T+P,C] -> [B,(T+P)//2+1,C] 傅里叶分解,奈奎斯特定理
frequency_list [(T+P)//2] 每个时间步振幅求峰值
frequency_list[0] = 0 直流分量赋值为 0 , 防止干扰最大周期识别
_, top_list = torch.topk(frequency_list, k) 找出周期振幅最明显的 top k 个,周期贡献度最高,得到的是索引值
top_list 转换类型
period = x.shape[1] // top_list 频率索引值转化为周期

frequency_list 频率能量值表

索引

$[0,1,2,3,4,5,....,\frac{T}{2}]=[0,1,2,3,4,....,48]$

频率(奈奎斯特定理,最后一个频率一定是 $\frac{1}{2}$ )

$[,\frac{1}{T},\frac{2}{T},\frac{3}{T},\frac{4}{T},......,\frac{1}{2}]$

对应的周期

$[,T,\frac{T}{2},\frac{T}{3},\frac{T}{4},\frac{T}{5},...,2]$

所以, 得到的返回的是最大索引, 通过 $\frac{时间步长度}{返回的索引值}=周期$

回到 Time block forward

见第二篇