TimesNet代码复现第二篇

在上一篇中

FFT_for_Period返回值示例输出

1
2
3


    def forward(self, x):
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)

FFT_for_Period 已经仔细的看过了

B, T, N = x.size() B=32,T+P=36,N=512

period_list, period_weight = FFT_for_Period(x, self.k)

period_list = array([ 6, 2, 9, 4, 36]) 周期贡献最高的五个周期分别等于 6,2,9,4,36

period_weight = 32 条时间序列 , 每个时间序列周期贡献最高的五个周期的振幅,都拿出来,注意,这里不是振幅,因为取了好几次平均

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


{Tensor: (32, 5)} tensor([[6.9830, 6.5103, 5.6676, 5.9629, 6.7698],
        [6.8133, 6.3813, 5.4634, 6.3629, 6.4095],
        [5.3253, 5.7509, 6.1553, 5.6881, 5.4701],
        [6.5091, 6.0778, 5.7477, 6.0265, 5.4799],
        [7.0926, 6.1656, 5.8321, 5.8032, 5.9332],
        [6.5665, 6.2172, 6.2676, 5.8920, 6.2983],
        [6.2408, 6.5438, 6.0920, 5.8592, 5.8397],
        [6.9564, 6.2190, 5.1747, 5.8705, 6.2396],
        [6.3966, 6.2373, 6.7544, 5.9575, 5.3530],
        [6.0948, 6.1206, 5.8837, 5.8999, 5.7880],
        [7.1670, 6.2935, 5.6127, 5.9107, 6.5963],
        [6.4346, 6.1183, 6.5684, 6.4988, 5.6983],
        [6.0550, 6.0338, 6.5007, 6.5481, 5.9036],
        [6.3313, 6.2670, 6.9504, 5.9295, 6.3365],
        [5.7959, 5.9147, 6.1357, 5.6044, 5.5584],
        [6.6410, 6.6974, 5.8965, 5.9663, 5.5961],
        [6.5233, 5.9610, 5.4359, 5.6711, 6.1382],
        [5.8449, 6.0800, 6.4006, 5.9664, 5.5951],
        [6.2470, 6.2729, 5.6796, 5.5737, 6.5849],
        [7.2218, 6.1741, 6.4214, 5.9840, 5.6851],
        [6.7487, 5.8529, 6.6712, 6.1054, 5.8511],
        [5.8093, 5.6079, 6.2193, 5.9004, 5.9107],
        [5.6643, 6.0798, 6.2897, 6.0147, 5.7959],
        [6.3037, 5.8968, 6.2462, 6.0778, 5.9490],
        [5.9308, 6.2217, 5.7885, 6.2411, 5.5404],
        [6.3786, 5.9597, 5.5894, 5.6784, 5.3526],
        [6.7759, 5.8732, 6.4847, 5.5802, 6.5243],
        [6.6263, 5.5450, 5.3019, 6.1780, 4.6952],
        [6.3923, 6.1576, 6.7257, 5.9322, 5.9460],
        [6.6944, 6.2269, 6.1482, 5.9639, 5.7772],
        [6.8458, 6.0419, 6.3469, 5.7175, 5.8940],
        [5.9458, 6.1565, 5.8753, 5.4544, 5.5671]], grad_fn=<IndexBackward0>)

精确的理解:

period_list = array([6, 2, 9, 4, 36]),这是通过FFT分析发现的5个最主要周期长度，即数据每隔6、2、9、4和36个时间步会出现一个完整的循环模式。
period_weight.shape = [32, 5], 确实是32条时间序列（批量大小）的权重,对每条序列，提取了5个主要周期的"能量值"（不完全等同于振幅）,更准确地说，这是每个序列在这5个主要频率上的平均能量贡献
frequency_list = abs(xf).mean(0).mean(-1) # 计算振幅平均值

① abs(xf)：计算FFT复数系数的模(振幅)

② .mean(0)：在批次维度上取平均

③ .mean(-1)：在特征维度上取平均

返回的第二个值 return period, abs(xf).mean(-1)[:, top_list] # [B, k]形状的张量

① 将每个样本的振幅(只取特征维度平均)在k个主要频率上的值返回

振幅(Amplitude)：对于复数FFT系数 $X_k = a_k + jb_k$，振幅是 $|X_k| = \sqrt{a_k^2 + b_k^2}$
能量(Energy)：频率分量的能量通常与振幅的平方成正比，即 $\text{Energy}_k \propto |X_k|^2$

for 循环

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


res = []
for i in range(self.k):
    period = period_list[i]
    # padding
    if (self.seq_len + self.pred_len) % period != 0:
        length = (
                         ((self.seq_len + self.pred_len) // period) + 1) * period
        padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
        out = torch.cat([x, padding], dim=1)
    else:
        length = (self.seq_len + self.pred_len)
        out = x
    # reshape
    out = out.reshape(B, length // period, period,
                      N).permute(0, 3, 1, 2).contiguous()
    # 2D conv: from 1d Variation to 2d Variation
    out = self.conv(out)
    # reshape back
    out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
    res.append(out[:, :(self.seq_len + self.pred_len), :])

先看明白的这里

1
2
3
4
5
6
7
8


else:
    length = (self.seq_len + self.pred_len)
    out = x
# reshape
out = out.reshape(B, length // period, period,
                  N).permute(0, 3, 1, 2).contiguous()
# 2D conv: from 1d Variation to 2d Variation
out = self.conv(out)

这里,period_list = array([ 6, 2, 9, 4, 36]),i = 0

(self.seq_len + self.pred_len) % period = 0 所以执行 else

length = (self.seq_len + self.pred_len) = 36

所以,out = x = [32,36,512] 发现周期=6

然后执行 reshape

1

out = out.reshape(B, length // period, period,N).permute(0, 3, 1,2).contiguous()

这里的变量存储, B, T, N = x.size() 批量,时间步长度,特征维度

发现周期=6.现在把时间步拆成 [32,6,6,512] , 第一个 6是 6 个周期,第二个 6 是每个周期 6 个时间步,permute 变换维度[32,512,6,6] , .contiguous() 保证内存连续,不破坏时间步的连续性

理论上更严谨的说法

将一维时间序列重新排列为二维矩阵
行数 = length // period（周期数）
列数 = period（每个周期的长度）
转换过程：
从 [批量, 时间步, 特征] 重塑为 [批量, 周期数, 周期长度, 特征], 通过permute转换为 [批量, 特征, 周期数, 周期长度]，适合2D卷积
实际意义：如果周期是24小时，那么每行代表一天的数据，整个矩阵表示多天的模式

1

            out = self.conv(out)

接下来是卷积

理论讲解: 二维卷积处理

应用Inception卷积模块捕获时间模式
能同时捕获周期内（列方向）和周期间（行方向）的关系
二维卷积天然适合处理这种排列成矩阵的周期性数据

重塑回一维序列

1
2


out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
res.append(out[:, :(self.seq_len + self.pred_len), :])

调整维度顺序为 [批量, 周期数, 周期长度, 特征]
重塑回一维序列 [批量, 时间步, 特征]
截取原始长度（去除可能的填充部分）

看这个卷积

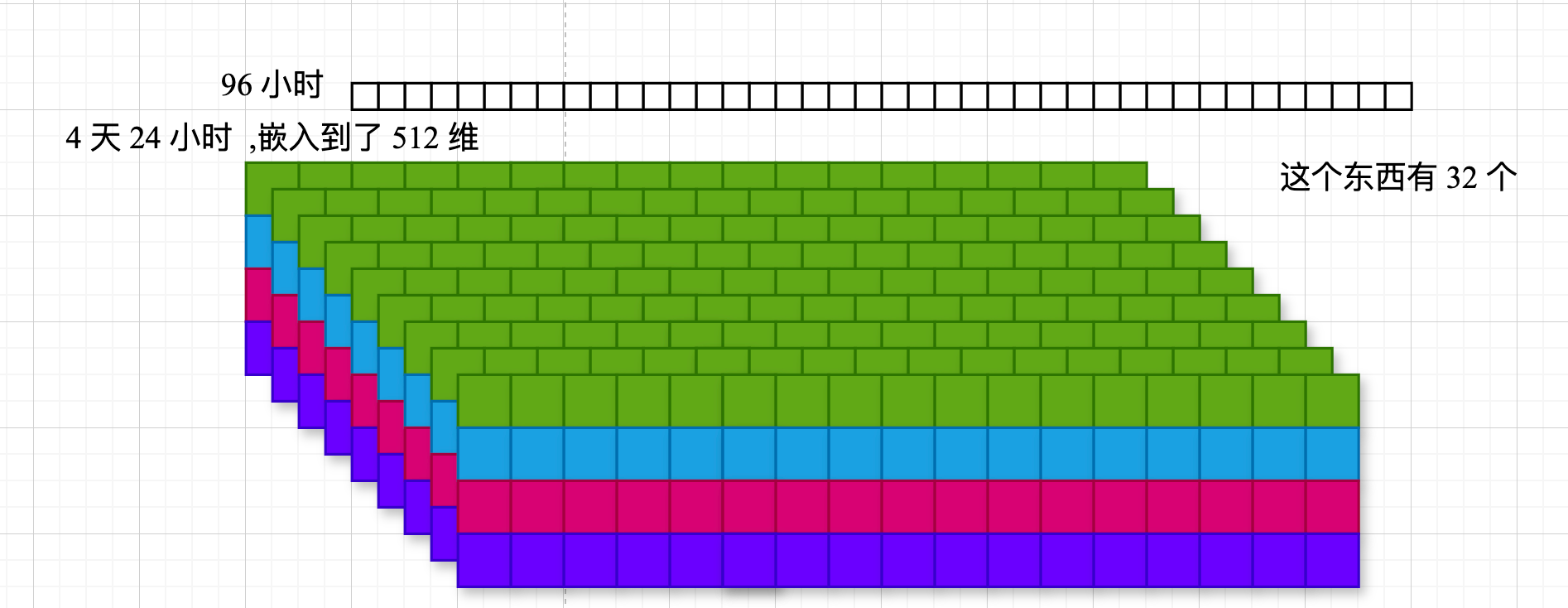
📝 图片描述: 有 512 张特征图,每个特征图尺寸是 4×24

Reshape：[32, 36, 512] → [32, 6, 6, 512]

32个样本
6个完整周期
每个周期包含6个时间步
512个特征维度

Permute(0, 3, 1, 2)：[32, 6, 6, 512] → [32, 512, 6, 6]

调整为卷积网络期望的输入格式：[批量, 通道, 高度, 宽度]
特征维度变为通道维度
周期数和周期长度变为空间维度
这种重塑实际上是将时间序列表示为"图像"：

每行代表一个完整周期（本例中是6个时间步）

共有6行，表示6个连续的周期
这种表示使2D卷积能够同时捕获：
周期内的局部模式（水平方向）
周期间的长期依赖（垂直方向）
这里文字例子是个正方形,但是图中特地画成矩形的, 后面注意看卷积是怎么做的

遗留问题

(1)conv 的处理

(2) padding

先看 padding

padding

1
2
3
4
5


# padding
if (self.seq_len + self.pred_len) % period != 0:
    length = (((self.seq_len + self.pred_len) // period) + 1) * period
    padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
    out = torch.cat([x, padding], dim=1)

先看例子, 假设 :

总序列长度 self.seq_len + self.pred_len = 100
发现的周期 period = 30

计算过程：

检查整除：100 % 30 = 10 ≠ 0，需要填充 if (self.seq_len + self.pred_len) % period != 0:
计算目标长度：(100 // 30 + 1) * 30 = (3 + 1) * 30 = 120 (length = (((self.seq_len + self.pred_len) // period) + 1) * period)
需填充长度：120 - 100 = 20 (padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]))
创建形状为[batch_size, 20, feature_dim]的零张量
拼接得到长度为120的序列 (out = torch.cat([x, padding], dim=1) 沿时间维度（dim=1）拼接原始数据和填充部分。)

还是拿例子对照着代码看得快

out = self.conv(out)

好了,开始看 1D 时间序列转二维, 卷积是怎么做的

这里是 Inception_Block_V1

步进 forward

1
2
3
4
5
6


def forward(self, x):
    res_list = []
    for i in range(self.num_kernels):
        res_list.append(self.kernels[i](x))
    res = torch.stack(res_list, dim=-1).mean(-1)
    return res

用自己的话说, 首先输入 x[32,512,18,2] 18 个周期为 2 的时序链

进入 for 循环 for i in range(self.num_kernels):

遍历卷积 List,有 6 层,

1
2
3
4
5
6
7
8


ModuleList(
  (0): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1))
  (1): Conv2d(512, 2048, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (2): Conv2d(512, 2048, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  (3): Conv2d(512, 2048, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
  (4): Conv2d(512, 2048, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
  (5): Conv2d(512, 2048, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))
)

分别经过 1×1 , 3×3,……,11 ×11 的卷积层, 卷积形状不变,输入通道数=512,输出通道数=2048

卷积核尺寸怎么来的

1
2
3


for i in range(self.num_kernels):
    kernels.append(nn.Conv2d(in_channels, out_channels, kernel_size=2 * i + 1, padding=i))
self.kernels = nn.ModuleList(kernels)

就是这样的嗷, 2 * i + 1 ,同时 padding=i 确保卷积前后的形状不变

每个卷积使用padding=i，确保输出形状一致
分别应用每个卷积核
将所有结果堆叠起来 res_list.**append**(self.kernels[i](x))
取平均值作为最终输出 res = torch.stack(res_list, dim=-1).mean(-1)

与周期性填充的关系

接上面的例子（周期=30，填充后长度=120）：
数据经过reshape和permute后，形状为[batch_size, features, 4, 30]（4个周期，每个周期30个时间步）
Inception_Block_V1同时考虑：
周期内关系：水平方向捕获每个周期内的模式
周期间关系：垂直方向捕获不同周期之间的模式

不同大小的卷积核对应不同大小的感受野：

小卷积核（如1×1）：捕获局部精细模式
大卷积核（如11×11）：捕获更大范围的时间依赖关系

num_kernels=6，会应用6个不同大小的卷积核:

i=0: 1×1卷积，padding=0
i=1: 3×3卷积，padding=1
i=2: 5×5卷积，padding=2
i=3: 7×7卷积，padding=3
i=4: 9×9卷积，padding=4
i=5: 11×11卷积，padding=5

每个卷积的输出形状都是[32, out_channels, 18, 2]，因为精心设计的padding保持了空间维度不变。

重要

res = torch.stack(res_list, dim=-1).mean(-1)

将6个形状为[32, 512, 18, 2]的张量堆叠

创建新的维度，得到形状[32, 512, 18, 2, 6]

.mean(-1)：

在最后一个维度(6个卷积结果)上取平均

输出形状恢复为[32, 512, 18, 2]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


输入: [32, 512, 18, 2]
  │
  ├─► 1×1卷积 ──► [32, 512, 18, 2]
  │
  ├─► 3×3卷积 ──► [32, 512, 18, 2]
  │
  ├─► 5×5卷积 ──► [32, 512, 18, 2]
  │
  ├─► 7×7卷积 ──► [32, 512, 18, 2]
  │
  ├─► 9×9卷积 ──► [32, 512, 18, 2]
  │
  └─► 11×11卷积 ─► [32, 512, 18, 2]
       │
       ▼
堆叠: [32, 512, 18, 2, 6]
       │
       ▼
平均: [32, 512, 18, 2]

这里的卷积的填充设置: (恰好滑动两次)

这些填充配置精确设计为能在宽度为2的输入上滑动恰好两次，保持输出尺寸与输入相同。

对于输入宽度=2，使用步长=1的卷积：

卷积核尺寸	填充大小	填充后宽度	滑动次数计算	输出宽度
1×1	0	2	(2-1)/1+1	2
3×3	1	4	(4-3)/1+1	2
5×5	2	6	(6-5)/1+1	2
7×7	3	8	(8-7)/1+1	2
9×9	4	10	(10-9)/1+1	2
11×11	5	12	(12-11)/1+1	2

滑动次数和输出高度和宽度相关

res = torch.stack(res_list, dim=-1).mean(-1)

调用torch.stack(res_list, dim=-1)时：

将6个形状为[32, 512, 18, 2]的张量

在新创建的最后一个维度上堆叠

得到形状为[32, 512, 18, 2, 6]的张量

这个6就表示从6个不同卷积核得到的6个特征图结果。随后的.mean(-1)操作会在这个维度上取平均，合并这6种不同尺度的特征。

这里涉及 torch.stack 的用法

torch.stack 的主要作用是增加一个新维度来合并张量。这是它与 torch.cat（连接张量但不增加维度）最关键的区别。

torch.stack 的工作原理

创建新维度：在指定位置创建一个全新的维度

张量要求：所有输入张量必须具有完全相同的形状

结果形状：输出张量的维度比输入张量多一个

1
2
3
4
5
6
7


# 假设有三个形状为 [2, 3] 的张量 a, b, c

# stack: 创建新维度
torch.stack([a, b, c], dim=0).shape  # [3, 2, 3]

# cat: 不创建新维度，在现有维度上连接
torch.cat([a, b, c], dim=0).shape    # [6, 3]

两个要点 ① torch.stack 是增加维度合并,注意区分和 torch.cat 的区别

②是,torch.stack 增加维度,没关系呀, .mean(-1) 维度又没咯

1
2
3
4
5
6


    def forward(self, x):
        res_list = []
        for i in range(self.num_kernels):
            res_list.append(self.kernels[i](x))
        res = torch.stack(res_list, dim=-1).mean(-1)
        return res

看完了,Inception_Block_V1 的处理,上面的文本图就很清楚了

最后再看一下卷积的配置吧

(1) 确保了输入和输出的空间维度保持完全一致。

维度保持机制详解

对于输入张量形状 [batch_size, in_channels, height, width]：

卷积层参数配置：

每个卷积核大小为 kernel_size=2*i+1

对应的填充为 padding=i

步长默认为1

空间维度计算：根据卷积公式: output_size = (input_size + 2*padding - kernel_size)/stride + 1

对于任意卷积 i：

output_height = (height + 2*i - (2*i+1))/1 + 1 = height

output_width = (width + 2*i - (2*i+1))/1 + 1 = width

通道维度变化：

输入通道数: in_channels=512

输出通道数: out_channels=2048

最终输出形状：

输入: [batch_size, in_channels, height, width]

输出: [batch_size, out_channels, height, width]

好了,回到 Time_Block forward

1

out = self.conv(out)

输入 out [32,512,18,2]
输出 out [32,512,18,2]

1

out = out.permute(0, 2, 3, 1).reshape(B, -1, N)

输入 out [32,512,18,2]
.permute(0, 2, 3, 1) [32,2,18,512]
.reshape(B, -1, N) [32,36,512]

1

res.append(out[:, :(self.seq_len + self.pred_len), :])

这里的截取长度的操作
padding 填充了这么多 , (length - (self.seq_len + self.pred_len))

① padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)),x.shape[2]]).to(x.device)

② out = torch.cat([x, padding], dim=1)

索引到 :(self.seq_len + self.pred_len) 即可

好了,

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


for i in range(self.k):
    period = period_list[i]
    # padding
    if (self.seq_len + self.pred_len) % period != 0:
        length = (
                         ((self.seq_len + self.pred_len) // period) + 1) * period
        padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
        out = torch.cat([x, padding], dim=1)
    else:
        length = (self.seq_len + self.pred_len)
        out = x
    # reshape
    out = out.reshape(B, length // period, period,
                      N).permute(0, 3, 1, 2).contiguous()
    # 2D conv: from 1d Variation to 2d Variation
    out = self.conv(out)
    # reshape back
    out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
    res.append(out[:, :(self.seq_len + self.pred_len), :])

这里的文本图:

假设输入x的形状为[B, T, N]，其中：

B: 批次大小(Batch size)
T: 时间序列长度(self.seq_len + self.pred_len)
N: 特征数量
周期为period

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


输入: [B, T, N] -> 例如: [32, 96+24, 7]
  │
  ▼
【填充处理】
  │  ┌─ 如果需要填充: [B, length, N] -> 例如: [32, 130, 7]
  └──┴─ 如果不需要填充: [B, T, N] -> 例如: [32, 120, 7]
  │
  ▼
【维度重塑】reshape成2D表示
  │  out.reshape(B, length//period, period, N)
  │  例如period=10: [32, 13, 10, 7]
  │
  ▼
【维度重排】permute以适应2D卷积
  │  out.permute(0, 3, 1, 2)
  │  [B, N, length//period, period]
  │  例如: [32, 7, 13, 10]
  │
  ▼
【2D卷积】Inception块处理
  │  self.conv(out)
  │  保持形状: [32, 7, 13, 10]
  │   ┌─► Inception_Block_V1 ──► [32, 7, 13, 10]
  │   │     内含多尺度卷积(1×1, 3×3, 5×5等)
  │   │
  │   ├─► GELU激活
  │   │
  │   └─► Inception_Block_V1 ──► [32, 7, 13, 10]
  │ 
  ▼
【维度恢复】
  │  out.permute(0, 2, 3, 1) -> [32, 13, 10, 7]
  │  out.reshape(B, -1, N) -> [32, 130, 7]
  │
  ▼
【截取原始长度】
  │  out[:, :T, :] -> [32, 120, 7]
  │
  ▼
循环k次后将结果保存在res列表中

后续

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


各周期结果res合并:
  │  torch.stack(res, dim=-1) -> [32, 120, 7, k]
  │  (k为周期数量)
  │
  ▼
加权聚合:
  │  利用period_weight进行加权
  │  [32, 120, 7, k] -> [32, 120, 7]
  │
  ▼
残差连接:
  │  res + x -> [32, 120, 7]

忘了,还是从头捋一遍

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


def forward(self, x):
    B, T, N = x.size()
    period_list, period_weight = FFT_for_Period(x, self.k)

    res = []
    for i in range(self.k):
        period = period_list[i]
        # padding
        if (self.seq_len + self.pred_len) % period != 0:
            length = (
                             ((self.seq_len + self.pred_len) // period) + 1) * period
            padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
            out = torch.cat([x, padding], dim=1)
        else:
            length = (self.seq_len + self.pred_len)
            out = x
        # reshape
        out = out.reshape(B, length // period, period,
                          N).permute(0, 3, 1, 2).contiguous()
        # 2D conv: from 1d Variation to 2d Variation
        out = self.conv(out)
        # reshape back
        out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
        res.append(out[:, :(self.seq_len + self.pred_len), :])
    res = torch.stack(res, dim=-1)
    # adaptive aggregation
    period_weight = F.softmax(period_weight, dim=1)
    period_weight = period_weight.unsqueeze(
        1).unsqueeze(1).repeat(1, T, N, 1)
    res = torch.sum(res * period_weight, -1)
    # residual connection
    res = res + x
    return res

第一句- 进来 B, T, N = x.size() 32,36(12→24),512

第二句period_list, period_weight = FFT_for_Period(x, self.k)

傅里叶分解, 32,19(直流分量+最小的周期是 2 个点一个周期),512

,选择前 5 个贡献度最高的周期,比如 3,7,12…

period_list 示例输出 array([ 6, 2, 9, 4, 36])

第三句 for i in range(self.k): for 循环遍历 top k 周期

period = period_list[i] 比如得到第一个最明显的周期 6

第四句,if 循环 if (self.seq_len + self.pred_len) % period != 0:

判断是不是被整除比如现在 36 识别的周期是 6 ,可以整除,执行 else

1

length = (self.seq_len + self.pred_len)

就是这句,也就是完整的周期长度

1

out = x

后面就是 out 的输出了

现在看 if 是怎么填充的

1
2
3
4
5


if (self.seq_len + self.pred_len) % period != 0:
    length = (
                     ((self.seq_len + self.pred_len) // period) + 1) * period
    padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
    out = torch.cat([x, padding], dim=1)

比如,周期识别到的是 7,长度是 36,那就得填充了,5 个周期=35,6 个周期=42,padding=42-35=7,然后 cat 上变成 32,42,512 去做卷积

1
2
3


# reshape
out = out.reshape(B, length // period, period,
                  N).permute(0, 3, 1, 2).contiguous()

接下来重塑形状,B,周期长度,周期数,512

permute 成 B,512,周期长度,周期数

1

out = self.conv(out)

接着卷积,捕捉周期内和周期间的相关关系,o,self.conv

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


Sequential(
  (0): Inception_Block_V1(
    (kernels): ModuleList(
      (0): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1))
      (1): Conv2d(512, 2048, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
      (2): Conv2d(512, 2048, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
      (3): Conv2d(512, 2048, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
      (4): Conv2d(512, 2048, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
      (5): Conv2d(512, 2048, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))
    )
  )
  (1): GELU(approximate='none')
  (2): Inception_Block_V1(
    (kernels): ModuleList(
      (0): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1))
      (1): Conv2d(2048, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
      (2): Conv2d(2048, 512, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
      (3): Conv2d(2048, 512, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
      (4): Conv2d(2048, 512, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4))
      (5): Conv2d(2048, 512, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5))
    )
  )
)

是这样的东西,这里是不变形状的卷积,(全是填充,但是我怀疑,这里你填这么多,肯定有误差)

1

 out = out.permute(0, 2, 3, 1).reshape(B, -1, N)

接下来恢复形状,[32,512,6 的周期长度,6 个周期数] permute 成 [32,6 的一个周期长度,6 个周期数,512 维度],reshape 成 [32,时间步长,512]

别晕,好好看看这里

1
2
3
4
5
6
7
8


    out = x
# reshape
out = out.reshape(B, length // period, period,
                  N).permute(0, 3, 1, 2).contiguous()
# 2D conv: from 1d Variation to 2d Variation
out = self.conv(out)
# reshape back
out = out.permute(0, 2, 3, 1).reshape(B, -1, N)

这里的 permute 或者 reshape 都是为了 self.conv 做准备的

[批次,时间步,特征]

reshape[批次,几个周期比如 4 天,一个周期长度 24 小时,特征维度]permute 成[批次,特征维度,4 天,24小时] 保证内存的连续性

好了,可以 conv 了,[4 天,24 小时]卷积把

捕捉好特征后,输出也是 [批次,512,4 天,24 小时] permute 成[批次,4 天,24 小时,512] reshape 成 [B,96 小时,512]

1

res.append(out[:, :(self.seq_len + self.pred_len), :])

一个周期的特征捕捉好了就存起来备用

96 个时间步,识别到 24 小时的周期,32 小时的周期 ….等等,res就 append 几次,这里就是 append topk 次

1

res = torch.stack(res, dim=-1)

stack 增加维度堆叠 [B,96 小时,512,使用的 topk 个周期]

接下来这里

1
2
3
4
5
6
7
8
9


res = torch.stack(res, dim=-1)
# adaptive aggregation
period_weight = F.softmax(period_weight, dim=1)
period_weight = period_weight.unsqueeze(
    1).unsqueeze(1).repeat(1, T, N, 1)
res = torch.sum(res * period_weight, -1)
# residual connection
res = res + x
return res

res = torch.stack(res, dim=-1) 这句话讲过了,堆叠成形状为[B, T, N, k]的张量，其中k是使用的周期数量（top_k）
后面讨论的对象都变成了 period_weight

这是 period_list, period_weight = FFT_for_Period(x, self.k) 的返回值

period_list的示例输出是

period_list = array([ 6, 2, 9, 4, 36]) 周期贡献最高的五个周期分别等于 6,2,9,4,36

period_weight = 32 条时间序列 , 每个时间序列周期贡献最高的五个周期的振幅,都拿出来,注意,这里不是振幅,因为取了好几次平均 ,形状是 [32,5]

period_weight 见本篇的开头

period_weight = F.softmax(period_weight, dim=1)

32 条时序链,每条链 96 个时间步,识别到的 top5 个周期能量,,96 个时间步浓缩成了 5 个周期,所以形状是 [32,5],也许从某种意义上说,96 个时间步被 5 个周期表示了,5 个周期的度量,是能量值

好了,继续 dim=1,[32,5]->[32,5] 同一个周期的 softmax,指数归一化

1
2


 period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)

[B,k]

① period_weight.unsqueeze(1) → [B, 1, k]

② period_weight.unsqueeze(1) → [B, 1, 1, k]

③ period_weight.repeat(1, T, N, 1) → [B, T, N, k]

[批次,top5 能量值] repeat [批次,96 时间步,512 维,5 个周期]

1

res = torch.sum(res * period_weight, -1)

这句, 加权聚合:res形状：[B, T, N, k]（批次、时间步、特征、周期数）

period_weight形状：[B, T, N, k]

res * period_weight：逐元素乘法，对每个周期应用其权重

torch.sum(…, -1)：沿着最后一个维度（周期维度）求和，得到[B, T, N]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


    def forward(self, x):
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)

        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (
                                 ((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
        res = torch.stack(res, dim=-1)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x
        return res

以实际例子讲解这个过程

第一句; B, T, N = x.size() 32,96 个时间步,512 维

第二句period_list, period_weight = FFT_for_Period(x, self.k)

识别到周期 (period_list)32,24,42 (period_weight) (32,24,42)在 32 条时间链的能量值(差不多振幅的平均吧)

第三句 for i in range(self.k): for循环

先是 if 条件句,将序列长度填充好周期长度的整数倍,不仔细看了

下一句 out = out.reshape(B, length // period, period, N).permute(0, 3, 1, 2).contiguous()

重塑形状 [32,4 天,24 小时,512] permute [32,512,4 天,24 小时]

out = self.conv(out) 分别对 [4 天,24 小时] 执行两次 1×1 卷积,3×3 卷积,5×5 卷积,7×7 卷积,11×11 卷积,这里补充一下,卷了这么多次是怎么融合结果的 res = torch.stack(res_list, dim=-1).mean(-1) stack 增加维度卷积,在 mean 又恢复维度了,就叫做融合了,回来,总之两句话吧①多尺度卷积,不变卷积②每个尺度卷积两次

out = out.permute(0, 2, 3, 1).reshape(B, -1, N) ,卷完了,[32,512,4 天,24 小时],32 是啥呢?第一个 4 天(1~~4 天),第二个 4 天(5~~8 天),(….),第 32 个 4 天,这是时序的样本组织形式,继续把,permute 成[32,4 天,24 小时,512 维],reshape 成[32,96 时间步,512 维]

res = torch.stack(res, dim=-1) 增加维度堆叠 [32,96 个时间步,512 维,5个周期尺度],不太好想象了,画图!还好是 4 维的

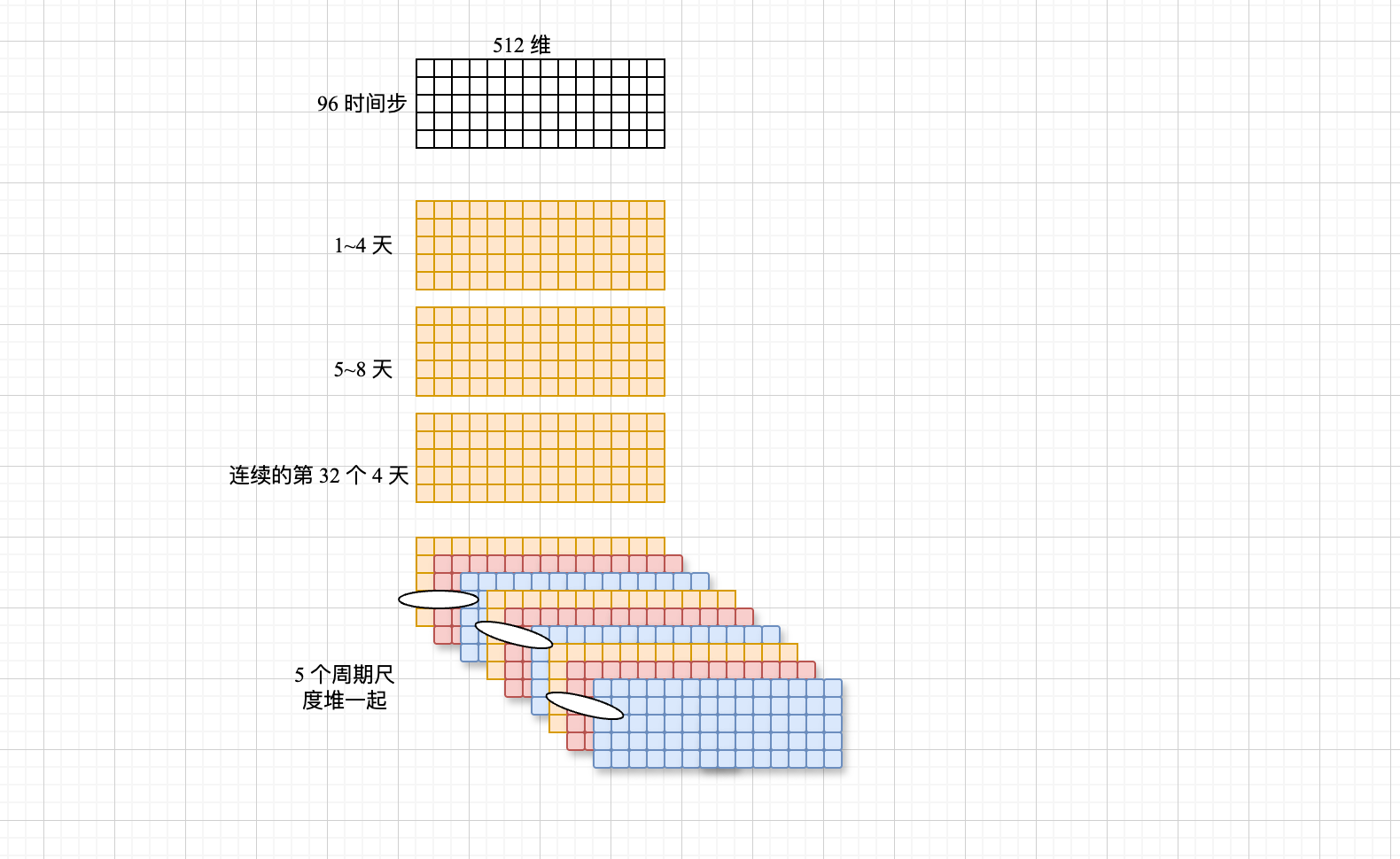
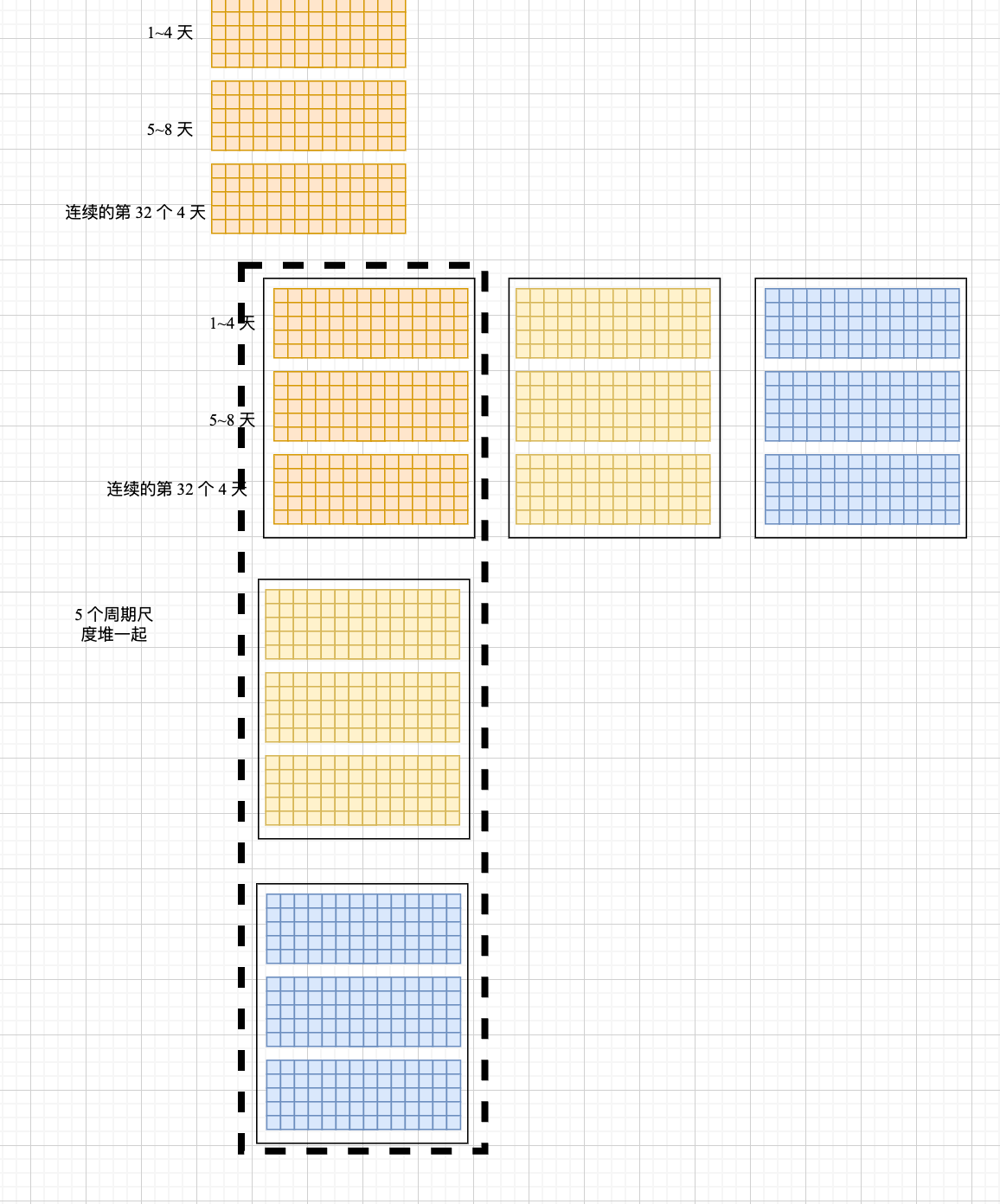
out = out.permute(0, 2, 3, 1).reshape(B, -1, N) ,[32,512,4 天,24 小时]

res = torch.stack(res, dim=-1) [32,96 个时间步,512 维,5个周期尺度]

5 个周期,分别不同尺度的卷,卷完了得到每个尺度卷完的结果,还是把 [32,96 个时间步,512 维] 看成一个表示

下一句: period_weight = F.softmax(period_weight, dim=1)

[32,5]1~4 天上,5 个尺度平均能量值 softmax 归一化一下

比如: [[0.3,05,0.2]

[0.1,0.7,0.4]]

下一句 period_weight = period_weight.unsqueeze( 1).unsqueeze(1).repeat(1, T, N, 1)

扩展维度,5 个平均能量值比如 24 小时的,32 小时的,42 小时的的能量值(3 个嘛)

32 个样本,每个样本 5 个周期的权重

复制,第0个样本,特征 0 的5 个权重值

第0个样本,特征 1 的5 个权重值

第0个样本,特征 512 的5 个权重值

第个样本,特征 0 的5 个权重值

第个样本,特征 1 的5 个权重值

第32个样本,特征 512 的5 个权重值

丢时间步了

哦,这里你得这么理解

1
2
3
4
5
6
7
8


# repeat前
[0.5, 0.3, 0.2]

# repeat后，变成了矩阵，每行都是相同的权重
[[0.5, 0.3, 0.2],
 [0.5, 0.3, 0.2],
 [0.5, 0.3, 0.2],
 ...（重复T×N次）]

重点在 （重复T×N次）

复制,第0个样本,第0个时间步,特征 0 的5 个权重值

第0个样本,第0个时间步,特征 1 的5 个权重值

第0个样本,第0个时间步,特征 512 的5 个权重值

,第0个样本,第0个时间步,特征 0 的5 个权重值

第0个样本,第96个时间步,特征 1 的5 个权重值

第0个样本,第0个时间步,特征 512 的5 个权重值

第32个样本,第0个时间步特征 0 的5 个权重值

第32个样本,第0个时间步,特征 1 的5 个权重值

第32个样本,第0个时间步,特征 512 的5 个权重值

第32个样本,第0个时间步特征 0 的5 个权重值

第32个样本,第96个时间步,特征 1 的5 个权重值

第32个样本,第96个时间步,特征 512 的5 个权重值

period_weight.unsqueeze(1).unsqueeze(1).repeat(1, T, N, 1)

1

[样本, 时间步, 特征, 周期权重]

具体来说：

对于第0个样本:
- 时间步0, 特征0: [w₀₁, w₀₂, w₀₃, w₀₄, w₀₅]
- 时间步0, 特征1: [w₀₁, w₀₂, w₀₃, w₀₄, w₀₅]
- …
- 时间步0, 特征511: [w₀₁, w₀₂, w₀₃, w₀₄, w₀₅]
- …
- 时间步95, 特征511: [w₀₁, w₀₂, w₀₃, w₀₄, w₀₅]
对于第1个样本:
- 所有位置: [w₁₁, w₁₂, w₁₃, w₁₄, w₁₅]

…以此类推直到第31个样本

这种设计确保了：

每个样本使用自己的周期权重（因为第一个维度不复制）
同一样本内的所有时间步和特征位置使用相同的周期权重
最终可以通过元素级乘法和求和，实现对不同周期特征的加权聚合

其实这里我还是有点理解的不透彻,就这样吧

终于来到了最后一步

1

res = torch.sum(res * period_weight, -1)

聚合

res.shape = torch.Size([32, 36, 512, 5])

period_weight.shape = ([32, 36, 512, 5]

对应位置相乘,在相加,形状变成 [32, 36, 512]

1

res = res + x

残差连接

1

 return res

返回,多巧,形状还是 [32, 36, 512]

回到 TimesNet forward

1
2
3


  # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))

执行两次TimesBlock处理。实现多层TimesBlock的堆叠

分层特征提取：不同层可以捕获不同尺度和复杂度的时间模式

📝 (重点在这儿)

较浅层可能捕获简单的周期性模式
较深层可以捕获更复杂的长期依赖关系

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# porject back
dec_out = self.projection(enc_out)

# De-Normalization from Non-stationary Transformer
dec_out = dec_out * \
          (stdev[:, 0, :].unsqueeze(1).repeat(
              1, self.pred_len + self.seq_len, 1))
dec_out = dec_out + \
          (means[:, 0, :].unsqueeze(1).repeat(
              1, self.pred_len + self.seq_len, 1))
return dec_out

感觉后面没啥好说的了

EncoderOnly 的结构

单向处理流程：数据经过嵌入层、多层TimesBlock处理，最后通过投影层输出结果
无解码器组件：没有使用Transformer典型的解码器结构（如交叉注意力、掩码自注意力等）
堆叠式架构：多个TimesBlock按顺序堆叠，类似于Transformer编码器中的多层结构
**不使用自注意力机制：**传统Transformer编码器依赖自注意力，而TimesNet使用FFT分析和2D卷积
周期性建模：通过FFT识别主要周期，将时间序列重新整形为二维表示进行处理

特征维度投影

1

dec_out = self.projection(enc_out)

看这儿

输入 enc_out [32,36,512] （批次大小, 时间步长, 特征维度）

self.projection Linear(in_features=512, out_features=7, bias=True)一个线性层换维度

dec_out [32,36,7] 将高维特征(512维)映射到低维输出空间(7维)，完成模型的特征提取

反归一化处理

1
2


dec_out = dec_out * (stdev[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1))
dec_out = dec_out + (means[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1))

对进行的归一化操作的逆运算，目的是将标准化后的值转换回原始数据尺度

乘以标准差

stdev[:, 0, :]：提取每个批次的标准差，形状为[32, 7]

.unsqueeze(1)：增加时间维度，形状变为[32, 1, 7]

.repeat(1, self.pred_len + self.seq_len, 1)：在时间维度上重复，形状变为[32, 36, 7]

dec_out * (…)：将每个位置的值乘以对应的标准差，恢复原始数据的"幅度" 加上均值

means[:, 0, :]：提取每个批次的均值，形状为[32, 7]

同样进行维度扩展成[32, 36, 7]

dec_out + (…)：将值加上对应的均值，恢复原始数据的"位置"

嗯,也是的 means 和 stdev 的维度是 [32,1,7] 都是在时间步维度上计算的

这里的 unsqueeze 是repeat 的操作不明白的….

在挣扎一下:

初始形状:

stdev的原始形状为[B, 1, C]

stdev[:, 0, :]取出每个批次的标准差，形状变为[B, C]

unsqueeze操作:

stdev[:, 0, :].unsqueeze(1) → 形状变为[B, 1, C]

这一步添加了一个"时间维度"的占位符

repeat操作:

.repeat(1, self.pred_len + self.seq_len, 1)参数含义：

第一个参数1: 在批次维度上不复制

第二个参数self.pred_len + self.seq_len: 在时间维度上复制此次数

第三个参数1: 在特征维度上不复制

结果形状: [B, self.pred_len + self.seq_len, C]

形象类比

想象有一个矩阵[[5, 6, 7]]，形状为[1, 3]：

**unsqueeze(0)**会增加第0维：

1

[[[5, 6, 7]]]  # 形状变为[1, 1, 3]

**repeat(2, 3, 1)**会复制：

1
2


[[[5, 6, 7], [5, 6, 7], [5, 6, 7]],  # 第一个复制的批次
 [[5, 6, 7], [5, 6, 7], [5, 6, 7]]]  # 第二个复制的批次

形状变为[2, 3, 3]

1
2
3
4


def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
    if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
        dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
        return dec_out[:, -self.pred_len:, :]  # [B, L, D]

dec_out[:, -self.pred_len:, :] # [B, L, D]

后面就截取出来预测长度,模型就完事咯

嗯,倒是提醒我还有一些疑问了,前面还没仔细看

见第三篇,查漏补缺