已经介绍过得通道注意力的变体:

• SENet
• SKNet
• CBAM
• CoorAttention

卷积三重注意力模块

WACV2021

也是通道注意力的变体之一

简介

尽管CBAM将通道注意力和空间注意力串联提供了更好的性能,但并没有考虑到跨维度交互,是彼此独立计算的

作者的意图:想要在不同的维度之间进行交互,探索空间和通道之间的关系,基于此本文提出了三重注意力,在三个分支上,分别考虑不同维度之间的交互

一个图像的shape,是$H×W×C$ ,3个分支的交互,就是H和W,H和C,W和C

此外与CBAM和SENet通过两层全连接层先降维后升维,这种方式来学习通道之间依赖性的做法相比,本文使用的是一种几乎无参数的注意力机制, 来建模通道和空间注意力,在不涉及降维的情况下,建立低成本有效的通道注意力

作者认为先降维后升维, 会导致通道间关系的损失,认为还是一对一直接对应的关系更好一些

结构图

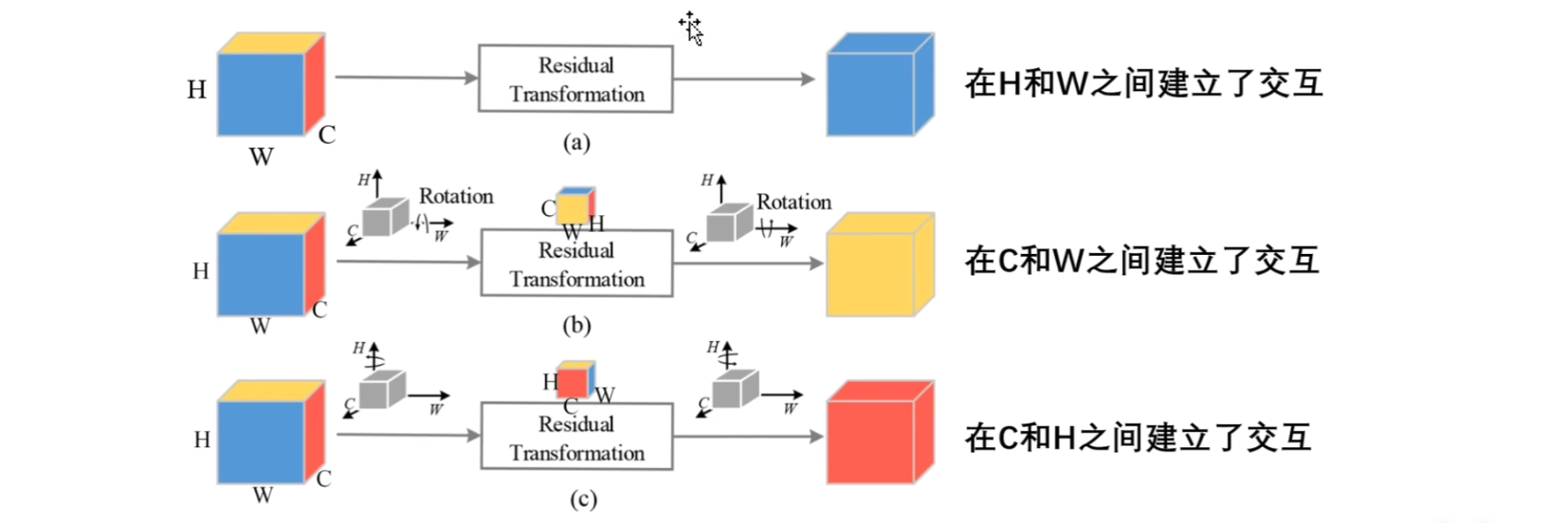
典型的三分支结构:

• 首先看输入和输出部分,第一个分支输出的是蓝色区域,意味着在原始图像的 H×W 层面上进行了交互
• 第二个分支输出的是黄色的区域,意味着在原始图像的 C×W 层面上进行了交互
• 第三个分支输出的是红色的区域,,意味着在原始图像的 C×H 层面上进行了交互

每一个分支都是一样的操作,都是先通过池化层,然后再通过卷积层,最后通过Sigmoid函数来生成权重,然后对输入进行特定维度上的调整

中间是相同的部分,不同的地方就在于它们分别是在不同的维度上来进行操作的

• 前两个分支都有旋转操作,

计算流程图

三分支结构

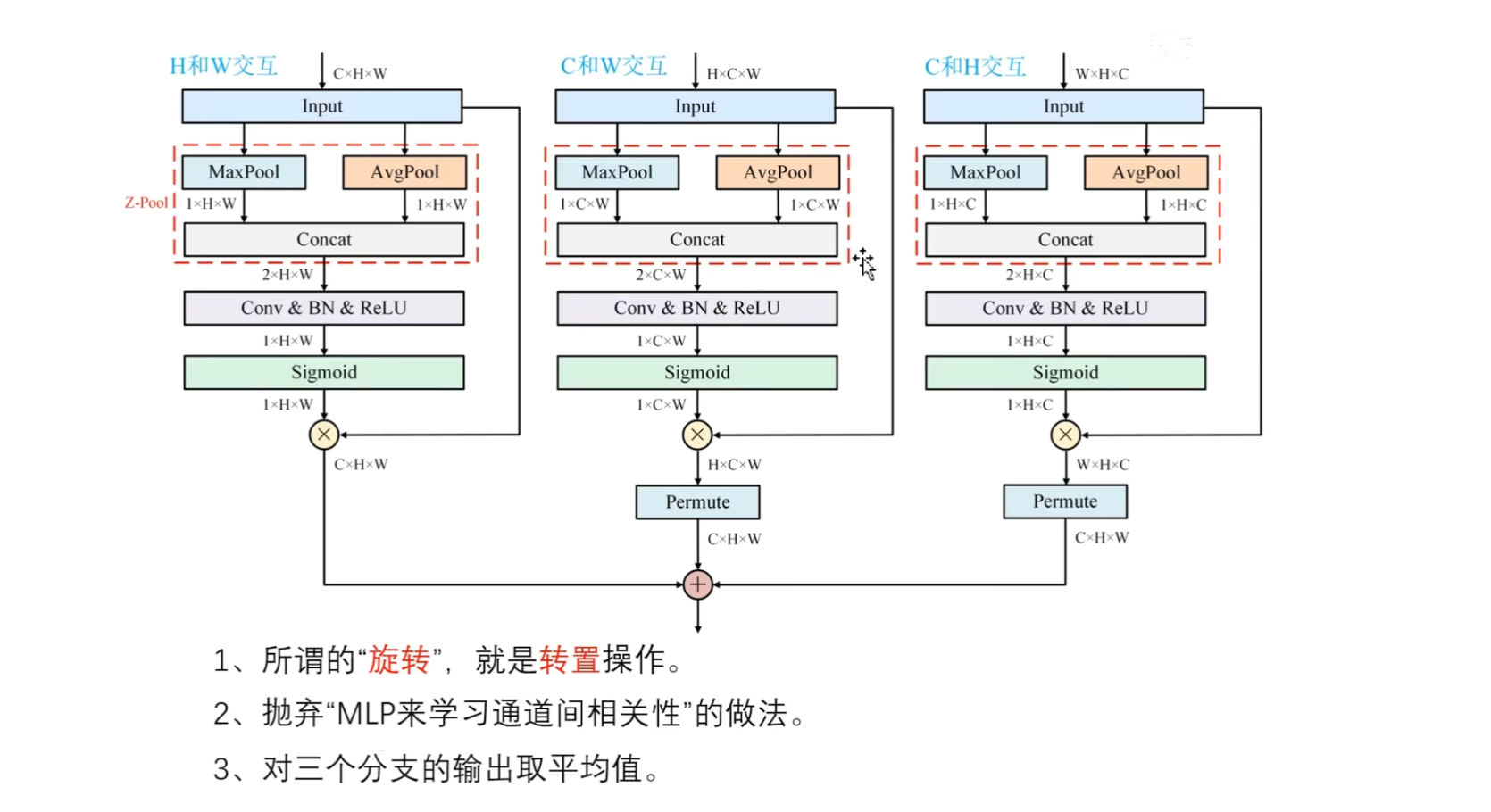
首先,三分支输入是相同的,shape是不一样的

• 第一个分支是CHW
• 第二个分支是HCW
• 第三个分支是WHC

进行了转置操作

以第一个分支为例

在H和W之间进行交互,也就是说要压缩C通道,只有压缩C通道才能够保留H和W

在H和W层面上的任意一个点,都具有横纵坐标,图中的 $Z-Pool $ 操作,就是通过最大池化和平均池化,然后对它们进行拼接,得到$2×H×W$的矩阵 ,然后再通过卷积操作,降维到 $1×H×W$

这里和CBAM中的空间注意力是一模一样的,都是直接把两个通道降维到一个通道,然后再通过Sigmoid函数来得到权重,从而来调整输入

• 同理,另外两个分支,分别是在C和W之间,C和H之间进行交互
• 唯一不同的就是在计算完成之后,需要通过一个维度转换,来重新恢复成C×H×W的形状,也是为了便于三个分支的输出,进行相加操作
  • 注意
  • (1)旋转操作,实际就是转置操作,通过permute函数来实现
  • (2)其次作者抛弃了MLP,来学习通道间相关性的做法,作者不学习通道间的相关性,让它们保持一一对应的关系
  • (3)对三个分支的输出,取平均值作为三重注意力模块的最终输出

接下来看:C和W交互,C和H交互

分别是在H维度上,W维度上进行压缩操作,十分类似于坐标注意力

对比坐标注意力

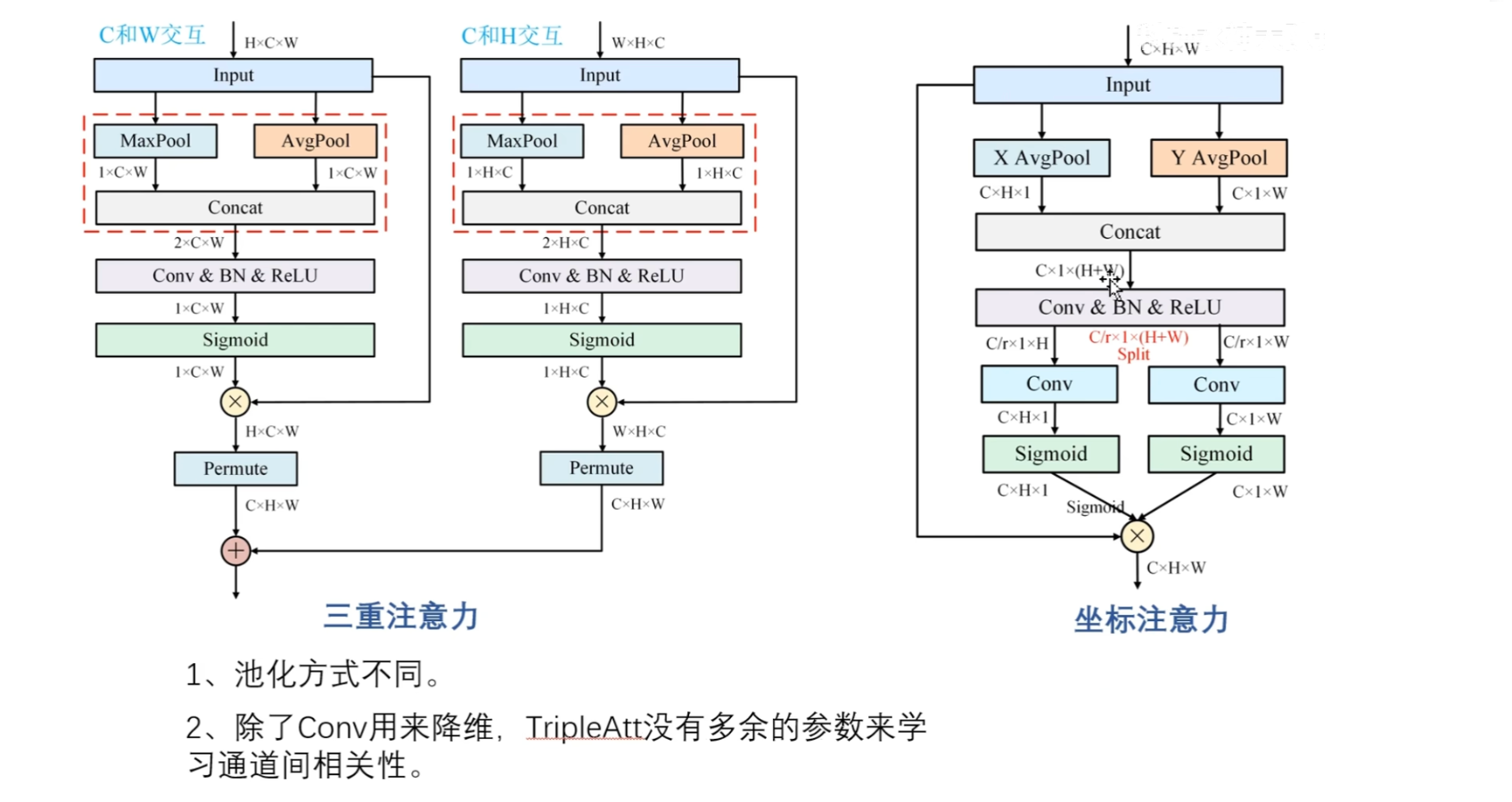
坐标注意力分别是在H方向和W方向上进行压缩,分别获得两个矩阵表示①C×H×1 ② C×1×W

然后在空间方向上,也就是H和W方向上进行拼接,得到$C×1×(H+W)$,再通过卷积层通过来降维,然后再通过卷积层来升维

最后再通过Sigmoid函数来获得权重,对输入进行特定维度上的调整

三重注意力和坐标注意力,除了中间的压缩操作以及映射设置方面稍微有一些不同之外整体上来说基本上是一致的

比如三重注意力的压缩操作使用的是最大池化和平均池化,然后再进行一个拼接,再进行一个降维操作

坐标注意力是对每一个方向,以W方向为例,是只使用一种池化也就是平均池化,然后通过卷积操作降维,然后再通过卷积再来升维

一些细节不同,整体上来说思想是一致的

这两篇论文,一篇是WACV2021,一篇的是CVPR2021

坐标注意力的写作

在三重注意力里面,作者说他们考虑了跨维度交互,然后通过三个分支分别对两两维度进行交互

在坐标注意力中,作者的写法:

沿着两个空间方向聚合为两个独立的方向感知特征图,每一个都捕捉了输入特征,沿着一个空间方向的长程依赖,并保留了另外一个空间方向的位置关系